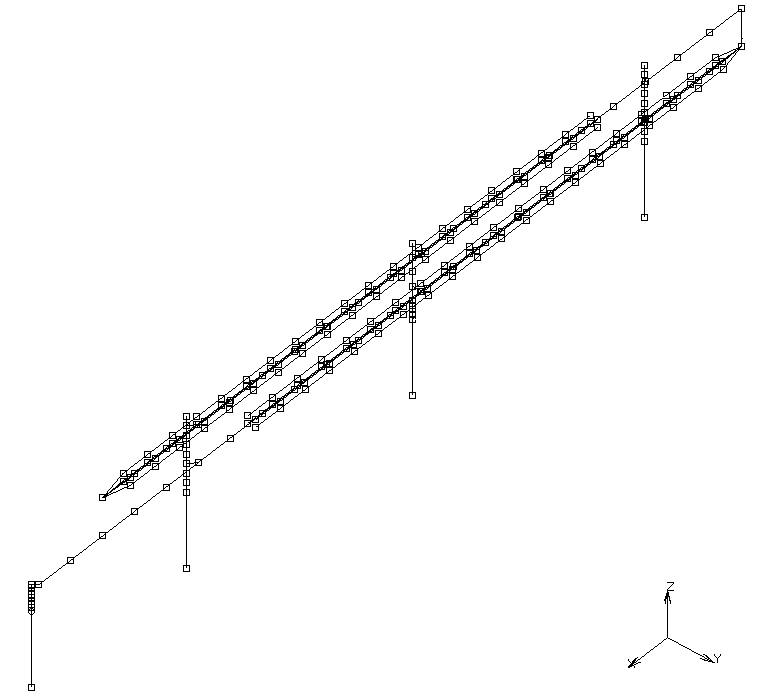Temperatur- und
Wärmestromberechnung der Antenne mit GFK- / Aluminium- Supports im CONSERT
-Experiment der ROSETTA-Mission
Einleitung
Die Antenne im CONSERT-Experiment
der ROSETTA-Mission muß einigen thermalen Spezifikationen genügen.
Bei der ‘verpackten’ Antenne ist die Einstrahlung bei einer Entfernung von
einem AU zu berücksichtigen. Bei der ‘ausgefahrenen’ Antenne sind die
Verhältnisse bei den Entfernungen 1,0, 3,0, und 5,25 AU zu
überprüfen. Ferner ist die Strahlungsrichtung zu beachten, die durch
den Polarwinkel q
beschrieben wird und immer in der xz-Ebene liegt.
So darf der gesamte Wärmestrom
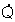 von den Supports zum Raumschiff den
Betrag von 2 W nicht überschreiten. Für die ‘verpackte’ Antenne
gilt eine weitere Spezifikation: Die Temperatur am Support 3 (50042) muß
bei einer Entfernung von einem AU im Bereich von -80 °C bis 100 °C
liegen. Von Interesse ist auch die Temperatur am Support 1 (50041) und die
Temperatur am Punkt, an dem sich der Dipol kreuzt.
von den Supports zum Raumschiff den
Betrag von 2 W nicht überschreiten. Für die ‘verpackte’ Antenne
gilt eine weitere Spezifikation: Die Temperatur am Support 3 (50042) muß
bei einer Entfernung von einem AU im Bereich von -80 °C bis 100 °C
liegen. Von Interesse ist auch die Temperatur am Support 1 (50041) und die
Temperatur am Punkt, an dem sich der Dipol kreuzt.
Bei dieser Berechnung werden GFK-Supports
berücksichtigt, die als Isolatoren zwischen Raumschiff und Antenne wirken.
Die Isolationswirkung ist im Anhang abgeschätzt. Support 1 und 3 bestehen
teilweise aus Aluminium.
Für die Berechnung wird die Methode der Finiten
Elemente (FE) angewandt. Die Wärmequellen und -senken durch
Wärmestrahlung erfordern eine Modellierung der Randbedingungen, so
daß eine Schnittstelle zur FE-Berechnung entsteht. Zur Realisierung
dieser Modellierung wird ein FORTRAN-Programm entwickelt, das auch die Ein-
und Ausgabe übernimmt.
Modellgrundlagen
Geometrie
- Abmessungen und Flächen
Die Strukturen der Antenne
bestehen aus Rohren und haben folgende Abmessungen (Tab. 1):
Tab. 1:
Abmessungen der Strukturen
|
Struktur |
Innenradius |
Außenradius |
Querschnitt |
Länge |
|
Struktur 1 (50044) |
8,06 mm |
9,95 mm |
106,94 mm² |
1100 mm |
|
Struktur 2 (50045) |
8,06 mm |
9,95 mm |
106,94 mm² |
1000 mm |
|
Reflektor (50046) |
2 mm |
2,5 mm |
7,069 mm² |
770 mm (4*) |
|
Dipol (50047) |
2 mm |
2,5 mm |
7,069 mm² |
770 mm (4*) |
Die Supports der Antenne haben eine komplexe
Gestalt. Die Temperaturen und die Wärmeströme werden durch die
gesamte freie Oberfläche bei der Abstrahlung und die Flächen in der
xy-Ebene und der yz-Ebene bei der Einstrahlung beeinflußt. Die
entsprechenden Flächen sind in Tab. 2 zusammengefaßt.
Tab. 2:
Oberflächen der Supports ohne MLI-Bedeckung
|
Struktur |
Oberfläche in xy-Ebene [m²] |
Oberfläche in yz-Ebene [m²] |
Oberfläche gesamt [m²] |
|
Support 1 (50040) GFK-Teil |
0 |
0,00123*5/8 |
0,0063*5/8 |
|
Support 1 (50040) Aluminium-Teil |
0,0014 |
0,00123*3/8 |
0,0063*3/8 |
|
Support 2 (50041) |
0,000135 |
0,0040 |
0,0141 |
|
Support 3 (50042) GFK-Teil |
0 |
0,0037/4 |
0,0240/4 |
|
Support 3 (50042) Aluminium-Teil |
0,00293 |
0,0037*3/4 |
0,0240*3/4 |
|
Support 4 (50043) |
0,000135 |
0,0040 |
0,0141 |
Der Materialgrenze
Aluminium / GFK der Supports 1 (3) liegt zwischen den Element 5 und 6
(4 und 5). Die Elementanzahl, Elementlänge und die Gesamtlänge der
Supportbereiche sind in Tab. 3 zusammengefaßt.
Tab. 3:
Elemente und Längen der Supports
|
Struktur |
Elementanzahl |
Elementlänge |
Gesamtlänge in z |
|
Support 1 (50040) GFK-Teil |
5 |
0,004375 |
0,0219 |
|
Support 1 (50040) Aluminium-Teil |
3 |
0,004375 |
0,0131 |
|
Support 2 (50041) |
8 |
0,0125 |
0,1 |
|
Support 3 (50042) GFK-Teil |
4 |
0,00625 |
0,025 |
|
Support 3 (50042) Aluminium-Teil |
4 |
0,01875 |
0,075 |
|
Support 4 (50043) |
8 |
0,0125 |
0,1 |
Die GFK-Bereiche der Supports werden durch zwei GFK-Platten der
Materialdicke 1,5 mm modelliert. Anhand der Breite kann die
xy-Queschnittsfläche berechnet werden, Tab. 4.
Tab. 4: Querschnitt der
Supports in xy-Ebene im GFK-Bereich
|
Struktur |
Materialdicke [m] |
GFK Gesamtbreite [m] |
Querschnittsfläche [m²] |
|
Support 1 (50040) |
0,0015 |
0,115 |
0,000173 |
|
Support 2 (50041) |
0,0015 |
0,09 |
0,000135 |
|
Support 3 (50042) |
0,0015 |
0,125 |
0,000188 |
|
Support 4 (50043) |
0,0015 |
0,09 |
0,000135 |
Orientierung der Antenne
Die Strukturen und Supports
haben eine Orientierung zum Koordinatensystem. Die Orientierung ist
entscheidend für die Einstrahlungsleistung. Bei den Strukturen CFK-Rohre,
Reflektor und Dipol ändert sich die Orientierung nach dem ‘Ausfahren’ der
Antenne. In den folgenden Tabellen werden die Orientierungen der Strukturen und
Supports als Einheitsvektoren angegeben (Tab. 5 und Tab. 6).
Tab. 5:
Orientierungsvektoren der Strukturen für die ‘verpackte’ und
‘ausgefahrene’ Antenne
|
Struktur |
Orientierung ‘verpackte’ Antenne |
Orientierung ‘ausgefahrene’ Antenne |
|
Struktur 1 (50044) |
(1,0,0) |
(0,1,0) |
|
Struktur 2 (50045) |
(1,0,0) |
(0,0,1) |
|
Reflektor (50046) |
(1,0,0) |
(,,0) |
|
Dipol (50047) |
(1,0,0) |
(,,0) |
Tab. 6:
Orientierungsvektoren der Supports (gilt nur wenn der Strahlungsvektor in der
xz-Ebene liegt)
|
Support |
Orientierung der xy-Ebene |
Orientierung der yz-Ebene |
|
Support 1 (50040) |
(1,0,0) |
(0,0,1) |
|
Support 2 (50041) |
(1,0,0) |
(0,0,1) |
|
Support 3 (50042) |
(1,0,0) |
(0,0,1) |
|
Support 4 (50043) |
(1,0,0) |
(0,0,1) |
Randbedingungen
- Schräge Einstrahlung auf die Antenne
Sind
 der Einheitsvektor der
Strahlungsrichtung und
der Einheitsvektor der
Strahlungsrichtung und 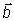 der
Orientierungsvektor der Struktur (siehe Abschnitt 2.1.2), dann ist der Anteil
f der einfallenden Strahlungsdichte
der
Orientierungsvektor der Struktur (siehe Abschnitt 2.1.2), dann ist der Anteil
f der einfallenden Strahlungsdichte
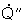 auf das Element:
auf das Element:
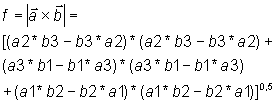 (1)
(1)
Der Einheitsvektor der Strahlungsrichtung ergibt sich aus
dem Polarwinkel q
:
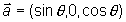 (2)
(2)
Dabei entspricht 0-Grad der z-Richtung .
Absorption von
Strahlungsenergie
Sind r der Radius der
Antennenstruktur, l die Länge der Struktur,
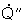 die einfallende Strahlungsdichte und
a
der Absorptionskoeffizient, dann ist die aufgenommene Strahlungsleistung P
der Struktur:
die einfallende Strahlungsdichte und
a
der Absorptionskoeffizient, dann ist die aufgenommene Strahlungsleistung P
der Struktur:
 (3)
(3)
Bem.:
- Die Strahlungsdichte
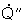
ist bei einer Punktquelle von der Entfernung d [in AU] abhängig.
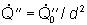 (4)
(4)
Dabei ist 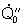 = 1344 W m-1 die Strahlungsdichte bei einem AU.
= 1344 W m-1 die Strahlungsdichte bei einem AU.
- Bei der ‘verpackten’ Antenne liegen die Strukturen
teilweise im Schatten anderer Strukturen. Diese Abschattung ist im Modell
berücksichtigt. Die Abschattung bewirkt eine Reduzierung der einfallenden
Strahlungsleistung (Tab. 7).
Tab. 7:
Reduzierung der Strahlungsleistung durch Abschattung für die ‘verpackte’
Antenne
|
Struktur |
Reduzierung der Strahlungsleistung durch
Abschattung |
|
Struktur 1 (50044) |
100 % |
|
Struktur 2 (50045) |
0 % |
|
Reflektor (50046) |
100 % |
|
Dipol (50047) |
50 % |
- Die Strahlungsleistung P auf die
Supports ergibt sich mit obigen Bezeichnungen zu:
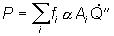 (5)
(5)
Dabei sind Ai die bestrahlten
Oberflächen der Supports und fi die zugehörigen
Anteile der Strahlungsleistung. Die Strahlungsleistung P wird verteilt
über jeweils acht Elemente in die Supports eingekoppelt.
- Wärmeabstrahlung
der Antenne im Weltall in der Nähe eines großen Objekts
Es wird davon ausgegangen,
daß die Antenne zur Hälfte das Weltall (T = 0
K) und zur anderen Hälfte ein Objekt ‘sieht’. Dies entspricht einem
Raumwinkel W
= 2 p
. Das Objekt hat die Temperatur TMLI (Tab. 8). Die von der
Antenne abgestrahlte Wärmeleistung P2 ergibt sich zu:
 (6)
(6)
Dabei ist e
der Emissionskoeffizient und T die Oberflächentemperatur.
Die Stefan-Boltzmann-Konstante hat den Wert
s
= 5,67 ×
10-8 W m-2 K-4.
Tab. 8: Temperatur der MLI
in Abhängigkeit von der Entfernung d
|
Entfernung d [AU] |
TMLI [K] |
|
1 |
358 |
|
3 |
258 |
|
5,25 |
98 |
Die Absorptions- und die Emissionsleistung in
den Materialbereichen der Supports wird gleichmäßig über die
vorhandenen Elemente verteilt.
-
Wärmewiderstände
Zwischen den Strukturen,
Supports und den Raumschiff treten Wärmewiderstände auf. Die
Wärmekopplungen sind für die ‘ausgefahrene’ und ‘verpackte’ Antenne
unterschiedlich (Tab. 9 und Tab. 10).
Tab. 9:
Wärmekopplungen zwischen den Elementen der ‘ausgefahrenen’ Antenne
|
Ort der Wärmekopplung |
Wert [W K-1] |
|
Wärmekopplung zwischen CFK-Struktur 1
(50044) und Reflektor (50046) |
¥
|
|
Wärmekopplung zwischen CFK-Struktur 2
(50045) und Dipol (50047) |
¥
|
|
Wärmekopplung zwischen CFK-Struktur 1
(50044) und CFK-Struktur 2 (50045) |
1,2 |
|
Wärmekopplung zwischen Support 1 (50040)
und CFK-Struktur 1 (50044) |
1,2 |
|
Wärmekopplung zwischen Raumschiff (S/C) und
Supports |
¥
|
Tab. 10:
Wärmekopplungen zwischen den Elementen der ‘verpackten’ Antenne
|
Ort der Wärmekopplung |
Wert [W K-1] |
|
Wärmekopplung zwischen CFK-Struktur 1
(50044) und Reflektor (50046) |
¥
|
|
Wärmekopplung zwischen CFK-Struktur 2
(50045) und Dipol (50047) |
¥
|
|
Wärmekopplung zwischen CFK-Struktur 1
(50044) und CFK-Struktur 2 (50045) |
0,003175 |
|
Wärmekopplung zwischen Support 1 (50040)
und CFK-Struktur 1 (50044) |
0,003175 |
|
Wärmekopplung zwischen Support 2 (50041)
und CFK-Struktur 1 (50044) |
¥
|
|
Wärmekopplung zwischen Support 2 (50041)
und CFK-Struktur 2 (50045) |
¥
|
|
Wärmekopplung zwischen Support 3 (50042)
und CFK-Struktur 1 (50044) |
¥
|
|
Wärmekopplung zwischen Support 3 (50042)
und CFK-Struktur 2 (50045) |
¥
|
|
Wärmekopplung zwischen Support 4 (50043)
und CFK-Struktur 1 (50044) |
¥
|
|
Wärmekopplung zwischen Support 4 (50043)
und CFK-Struktur 2 (50045) |
¥
|
|
Wärmekopplung zwischen Raumschiff (S/C) und
Supports |
¥
|
Bem.:
- Die ‘Wärmekopplung zwischen CFK-Struktur 1 (50044)
und CFK-Struktur 2 (50045)’ und die ‘Wärmekopplung zwischen Support 1
(50040) und CFK-Struktur 1 (50044)’ werden durch Federgelenke bestimmt
(siehe Anhang).
- Die Temperatur am Raumschiff TSC
[K] ist von der Entfernung abhängig (Tab. 11).
Tab. 11:
Temperatur des Raumschiffs in Abhängigkeit von der Entfernung d
|
Entfernung d [AU] |
TSC [K] |
|
1 |
313 |
|
3 |
273 |
|
5,25 |
236 |
Materialkennwert
- Wärmeleitfähigkeit
Die Supports, CFK-Strukturen,
der Dipol und der Reflektor bestehen aus verschiedenen Materialien und haben
deshalb unterschiedliche Wärmeleitfähigkeiten (Tab. 12).
Tab. 12:
Wärmeleitfähigkeit der Elemente
|
Element |
Wärmeleitfähigkeit [W m-1
K-1] |
|
Struktur 1 (50044) |
36,5 (siehe Anhang) |
|
Struktur 2 (50045) |
36,5 (siehe Anhang) |
|
Reflektor (50046) |
145 |
|
Dipol (50047) |
145 |
|
Support 1 (50040) GFK-Teil |
0,4 |
|
Support 1 (50040) Aluminium-Teil |
145 |
|
Support 2 (50041) |
0,4 |
|
Support 3 (50042) GFK-Teil |
0,4 |
|
Support 3 (50042) Aluminium-Teil |
145 |
|
Support 4 (50043) |
0,4 |
Bem.:
- Die CFK-Strukturen sind gefüllt. Das
Füllmaterial beeinflußt die Temperatur und Wärmeströme
nicht, da die Wärmeleitfähigkeit des Füllmaterials wesentlich
schlechter ist als die des CFK-Rohrs (siehe Anhang).
- Die CFK-Rohre sind mit einer Aluminiumfolie der
Stärke 0,1 mm als Plasmocerträger beschichtet. Die
Wärmeleitfähigkeit der Strukturen 1 und 2 beträgt
l
= 36,5 W m-1 K-1
(siehe Anhang).
Absorptions- und
Emissionskoeffizient
Tab. 13: Absorptions- und
Emissionskoeffizient
|
Oberfläche |
Absorptionskoeffizient
a
|
Emissionskoeffizient
e
|
|
Weißes Plasmocer |
0,34 |
0,76 |
|
Schwarzes Plasmocer |
0,91 |
0,77 |
|
‘Schwarze Farbe’ (GFK-Oberfläche)
|
0,95 |
0,85 |
Modellannahme
Alle vier Grundplatten der Supports
sind MLI-bedeckt. Wäre das nicht der Fall, kann die Oberfläche der
Aluminium-Grundplatten Wärme abstrahlen und auch durch Einstrahlung
Energie aufnehmen. Nachfolgend sind für eine Grundfläche von
77 cm die Abstrahlung und die Einstrahlung berechnet. Dabei sind die
Oberflächen mit schwarzen Plasmocer beschichtet und haben die gleiche
Temperatur wie das Raumschiff TSC (Tab. 11) .
d[AU]: 1,00 Theta: 0,00 Abstrahlung[W]: 3,23 Einstrahlung[W]: 9,42
Bilanz[W]: 6,19
d[AU]: 1,00 Theta: 15,00 Abstrahlung[W]: 3,23 Einstrahlung[W]: 9,10 Bilanz[W]: 5,87
d[AU]: 1,00 Theta: 30,00 Abstrahlung[W]: 3,23 Einstrahlung[W]: 8,16 Bilanz[W]: 4,93
d[AU]: 1,00 Theta: 45,00 Abstrahlung[W]: 3,23 Einstrahlung[W]: 6,66 Bilanz[W]: 3,43
d[AU]: 1,00 Theta: 60,00 Abstrahlung[W]: 3,23 Einstrahlung[W]: 4,71 Bilanz[W]: 1,48
d[AU]: 1,00 Theta: 75,00 Abstrahlung[W]: 3,23 Einstrahlung[W]: 2,44 Bilanz[W]: -0,79
d[AU]: 1,00 Theta: 90,00 Abstrahlung[W]: 3,23 Einstrahlung[W]: 0,00 Bilanz[W]: -3,23
d[AU]: 3,00 Theta: 0,00 Abstrahlung[W]: 1,87 Einstrahlung[W]: 1,05 Bilanz[W]: -0,82
d[AU]: 3,00 Theta: 15,00 Abstrahlung[W]: 1,87 Einstrahlung[W]: 1,01 Bilanz[W]: -0,86
d[AU]: 3,00 Theta: 30,00 Abstrahlung[W]: 1,87 Einstrahlung[W]: 0,91 Bilanz[W]: -0,96
d[AU]: 3,00 Theta: 45,00 Abstrahlung[W]: 1,87 Einstrahlung[W]: 0,74 Bilanz[W]: -1,13
d[AU]: 3,00 Theta: 60,00 Abstrahlung[W]: 1,87 Einstrahlung[W]: 0,52 Bilanz[W]: -1,34
d[AU]: 3,00 Theta: 75,00 Abstrahlung[W]: 1,87 Einstrahlung[W]: 0,27 Bilanz[W]: -1,60
d[AU]: 3,00 Theta: 90,00 Abstrahlung[W]: 1,87 Einstrahlung[W]: 0,00 Bilanz[W]: -1,87
d[AU]: 5,25 Theta: 0,00 Abstrahlung[W]: 1,04 Einstrahlung[W]: 0,34 Bilanz[W]: -0,70
d[AU]: 5,25 Theta: 15,00 Abstrahlung[W]: 1,04 Einstrahlung[W]: 0,33 Bilanz[W]: -0,71
d[AU]: 5,25 Theta: 30,00 Abstrahlung[W]: 1,04 Einstrahlung[W]: 0,30 Bilanz[W]: -0,75
d[AU]: 5,25 Theta: 45,00 Abstrahlung[W]: 1,04 Einstrahlung[W]: 0,24 Bilanz[W]: -0,80
d[AU]: 5,25 Theta: 60,00 Abstrahlung[W]: 1,04 Einstrahlung[W]: 0,17 Bilanz[W]: -0,87
d[AU]: 5,25 Theta: 75,00 Abstrahlung[W]: 1,04 Einstrahlung[W]: 0,09 Bilanz[W]: -0,95
d[AU]: 5,25 Theta: 90,00 Abstrahlung[W]: 1,04 Einstrahlung[W]: 0,00 Bilanz[W]: -1,04
Sind die Aluminium-Grundplatten mit
weißem Plasmocer beschichtet ergeben sich folgende Werte:
d[AU]: 1,00 Theta: 0,00 Abstrahlung
[W]: 3,18 Einstrahlung[W]: 3,52 Bilanz[W]: 0,33
d[AU]: 1,00 Theta: 15,00 Abstrahlung[W]: 3,18 Einstrahlung[W]: 3,40 Bilanz[W]: 0,21
d[AU]: 1,00 Theta: 30,00 Abstrahlung[W]: 3,18 Einstrahlung[W]: 3,05 Bilanz[W]: -0,14
d[AU]: 1,00 Theta: 45,00 Abstrahlung[W]: 3,18 Einstrahlung[W]: 2,49 Bilanz[W]: -0,70
d[AU]: 1,00 Theta: 60,00 Abstrahlung[W]: 3,18 Einstrahlung[W]: 1,76 Bilanz[W]: -1,43
d[AU]: 1,00 Theta: 75,00 Abstrahlung[W]: 3,18 Einstrahlung[W]: 0,91 Bilanz[W]: -2,27
d[AU]: 1,00 Theta: 90,00 Abstrahlung[W]: 3,18 Einstrahlung[W]: 0,00 Bilanz[W]: -3,18
d[AU]: 3,00 Theta: 0,00 Abstrahlung[W]: 1,84 Einstrahlung[W]: 0,39 Bilanz[W]: -1,45
d[AU]: 3,00 Theta: 15,00 Abstrahlung[W]: 1,84 Einstrahlung[W]: 0,38 Bilanz[W]: -1,47
d[AU]: 3,00 Theta: 30,00 Abstrahlung[W]: 1,84 Einstrahlung[W]: 0,34 Bilanz[W]: -1,50
d[AU]: 3,00 Theta: 45,00 Abstrahlung[W]: 1,84 Einstrahlung[W]: 0,28 Bilanz[W]: -1,57
d[AU]: 3,00 Theta: 60,00 Abstrahlung[W]: 1,84 Einstrahlung[W]: 0,20 Bilanz[W]: -1,65
d[AU]: 3,00 Theta: 75,00 Abstrahlung[W]: 1,84 Einstrahlung[W]: 0,10 Bilanz[W]: -1,74
d[AU]: 3,00 Theta: 90,00 Abstrahlung[W]: 1,84 Einstrahlung[W]: 0,00 Bilanz[W]: -1,84
d[AU]: 5,25 Theta: 0,00 Abstrahlung[W]: 1,03 Einstrahlung[W]: 0,13 Bilanz[W]: -0,90
d[AU]: 5,25 Theta: 15,00 Abstrahlung[W]: 1,03 Einstrahlung[W]: 0,12 Bilanz[W]: -0,91
d[AU]: 5,25 Theta: 30,00 Abstrahlung[W]: 1,03 Einstrahlung[W]: 0,11 Bilanz[W]: -0,92
d[AU]: 5,25 Theta: 45,00 Abstrahlung[W]: 1,03 Einstrahlung[W]: 0,09 Bilanz[W]: -0,94
d[AU]: 5,25 Theta: 60,00 Abstrahlung[W]: 1,03 Einstrahlung[W]: 0,06 Bilanz[W]: -0,97
d[AU]: 5,25 Theta: 75,00 Abstrahlung[W]: 1,03 Einstrahlung[W]: 0,03 Bilanz[W]: -1,00
d[AU]: 5,25 Theta: 90,00 Abstrahlung[W]: 1,03 Einstrahlung[W]: 0,00 Bilanz[W]: -1,03
Ergebnis:
Die Bilanz zwischen Einstrahlung und Abstrahlung nimmt
Werte zwischen -3,2 W und 6,2 W bei schwarzer Plasmocer-Beschichtung
bzw. zwischen -3,2 W und 0,3 W bei weißer Plasmocer-
Beschichtung an. Ein Bedeckung der Grundplatten mit MLI unterdrückt die
Strahlungsleitung total und ist wegen der Wärmestrom-Spezifikation
erforderlich.
Bemerkungen:
- Die Berechnung erfolgt mit der Annahme, daß die
Oberfläche ‘frei’ liegt. Das bedeutet, daß die Antennenstruktur
weder die Grundfläche bei der Einstrahlung abschattet noch die
Wärmeabstrahlung behindert.
- Es ist zu beachten, daß die hier berechneten
Wärmeströme zusätzlich zu den aus den GFK-Werkstoffen wirken.
Berechnung
Physikalische Grundlage:
Wärmeleitungsgleichung
Zur Temperaturfeldberechnung
dient die Wärmeleitungsgleichung
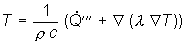 (7)
(7)
Darin ist:
c spezifische Wärmekapazität,
[J kg-1 K-1]
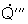 volumenbezogener Wärmestrom
an der Quelle/Senke, [W m-3]
volumenbezogener Wärmestrom
an der Quelle/Senke, [W m-3]
T Temperatur, [K]
l
Wärmeleitfähigkeit, [W m-1 K-1
]
r
Dichte, [kg m-3]
Numerische Lösung
Die Temperatur wird solange
berechnet bis obige Wärmeleitungsgleichung stationär wird. Die
Materialkennwerte Dichte und spezifische Wärmekapazität haben keinen
Einfluß auf die stationäre Temperaturverteilung und auf die
Wärmeströme. Diese Materialkennwerte bestimmen aber die Zeit, bis
die Wärmeleitungsgleichung stationär wird. Als Rechenwerte werden
realistische Materialkennwerte verwendet [1].
Zur Lösung der Differentialgleichung wird das
Finite-Element-Programm MARC K7.2 eingesetzt. Ein FE-Netz ist zur Anwendung
der Finite-Element-Methode notwendig (siehe Anhang).
Ergebnisse
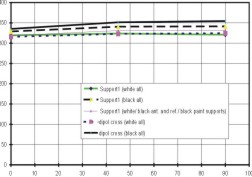
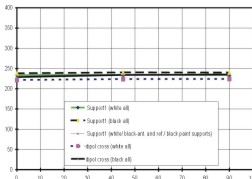
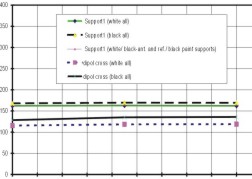
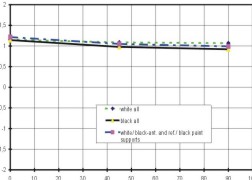
Folgende Berechnungen wurden
durchgeführt und in Excel dokumentiert (Tab. 14):
Tab. 14:
Berechnungen und Dateien
|
Dateien
(Antenne ‘verpackt’) |
Dateien
(Antenne ‘ausgefahren’) |
Bemerkungen |
|
Stowed_white_alu_cap.xls |
disploy_white_alu_cap.xls |
Die Aluminium Teile der Supports 1 und 3 sind
mit weißen Plasmocer beschichtet |
|
Stowed_black_alu_cap.xls |
disploy_black_alu_cap.xls |
Die Aluminium Teile der Supports 1 und 3 sind
mit schwarzem Plasmocer beschichtet |
Bemerkung zu den Meßergebnissen:
- Die Grundplatten der Supports sind zu 100% mit MLI
bedeckt, sonst keine MLI-Bedeckung der Antenne
- Lage der Temperaturmeßpunkte:
Support 1: im GFK-Bereich
Support 3: an der Grenze GFK/Aluminium
Fazit:
Die Spezifikationen sind erfüllt, falls folgende
Konfiguration vorliegt:
- die Aluminium-Grundplatten sind mit MLI bedeckt;
- der Dipol und der Reflektor sind mit schwarzen
Plasmocer bedeckt;
- die Strukturen 1 und 2 und die Aluminiumoberflächen
der Supports sind mit weißem Plasmocer bedeckt;
- die GFK-Oberflächen der Support sind schwarz
gestrichen.
Anhang
Geringe Wärmeleitung
der Supports
Alle vier Supports haben eine
geringe effektive Leitfähigkeit längs der z-Achse. Grund: Die
Wärmeleitfähigkeit des GFK-Materials ist mit
l
= 0,4 W m-1 K-1 klein und der
Querschnitt A in der xy-Ebene beträgt zusammen 0,000631 m².
Die effektive Leitfähigkeit berechnet sich zu:
 (8)
(8)
Dabei ist:
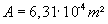 (9)
(9)
Es ergibt sich bei einer GFK Isolationslänge l
= 0,025 m und l
= 0,4 W m-1 K-1:
 (10)
(10)
Das bedeutet, daß bei einer Temperaturdifferenz von
100K über die Gesamtlänge 2,5 cm der Wärmestrom über
alle vier Supports nur 1,0 W beträgt.
Wärmeleitfähigkeit des CFK-Rohr
Das CFK-Rohr ist aus drei
unterschiedlichen Materialien aufgebaut. Die Wärmeleitfähigkeit
l
CFK kann aus den einzelnen Wärmeleitfähigkeiten
der Komponenten (Tab. 15) berechnet werden (siehe Gleichung (11)). Es ergibt
sich eine Wärmeleitfähigkeit von 30,1 W m-1 K
-1, falls l
GFK =0,4 W m-1 K-1
ist.
Tab. 15:
Daten des CFK-Rohr-Aufbaus
|
Material |
rinnen [m] |
raußen [m] |
l
[W m-1 K-1] |
Querschnittsfläche A [m²] |
|
M40 |
0,00806 |
0,00920 |
50 |
6,18 ×
10-5 |
|
GFK |
0,00920 |
0,00935 |
0,4 |
8,74 ×
10-6 |
|
T300 |
0,00935 |
0,00995 |
3,46 |
3,64 ×
10-5 |
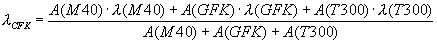 &#
9;(11)
&#
9;(11)
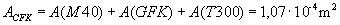 (12)
(12)
Für die Leitfähigkeit lfCFK der
Struktur gilt:
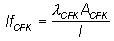 (13)
(13)
Bei einer Länge von einem Meter ergibt sich eine
Leitfähigkeit von 3,22 ×
10-3 W K-1.
Bemerkung:
Falls die unbekannte Größe l
GFK =20,0 W m-1 K-1
ist, würde die Wärmeleitfähigkeit auf 31,7 W m-
1 K-1 ansteigen. Für Glasfaser verstärkte
Kunststoffe ist die Wärmeleitfähigkeit geringer als verstärkte
mit ungerichteter Faser [1].
Schlechte
Wärmeleitung in der Füllung der CFK-Strukturen
Aufgrund der schlechten
Wärmeleitfähigkeit der Füllung von den CFK-Strukturen erfolgt
die Wärmeleitung vorwiegend durch das CFK-Material. Denn es gilt für
die Leitfähigkeit lf längs der Rohrrichtung
 (14)
(14)
Dabei ist:
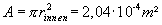 (15)
(15)
Es ergibt sich bei l = 1 m und
l
= 0,04 W m-1 K-1:
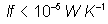 (16)
(16)
Dieser Wert ist um 2 Größenordnungen kleiner als
lfCFK!
Wärmeleitfähigkeit der Federgelenke
Zwischen den Support 1 (50040)
und der Struktur 1 (50044) und auch zwischen Struktur 1 (50044) und Struktur 2
(50045) befindet sich ein Federgelenk. Dieses Federgelenk besteht aus vier
Stahlstreifen mit folgenden Maßen (Tab. 16):
Tab. 16:
Maße der Federgelenke
|
Länge l: |
80 mm |
|
Breite b: |
12,7 mm |
|
Dicke d: |
0,1 mm |
Mit einer Wärmeleitfähigkeit von
Stahl l
Stahl = 50 W m-1 K-1
[1] ergibt sich für die Leitfähigkeit des Federgelenks in
Längsrichtung:
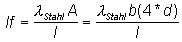 (17)
(17)
Das ergibt einen Wert von lf = 0,
003175 W K-1.
Wärmeleitfähigkeit des Plasmocerträger auf der CFK-Struktur
Die CFK Strukturen (50044 und
50045) sind mit einer Aluminiumfolie als Plasmocerträger beschichtet. Die
Aluminiumfolie hat eine Dicke von 0,1 mm. Mit einer
Wärmeleitfähigkeit von Aluminium l
Aluminium = 145 W m-1
K-1 [1] ergibt sich für die Leitfähigkeit der
Struktur in Längsrichtung:
 (18)
(18)
Das ergibt einen Wert von lf = 9,074
×
10-4 W K-1 bei einer
Querschnittsfläche AAluminium = 6,25
×
10-6 m² und einer Länge von einem Meter.
Es ergibt sich durch Rechnung analog zur Gleichung (11)
eine Wärmeleitfähigkeit der Struktur von 36,5 W m-1
K-1.
FE-Netze

Abb. 1: FE-Netz für die
‘ausgefahrene’ Antenne
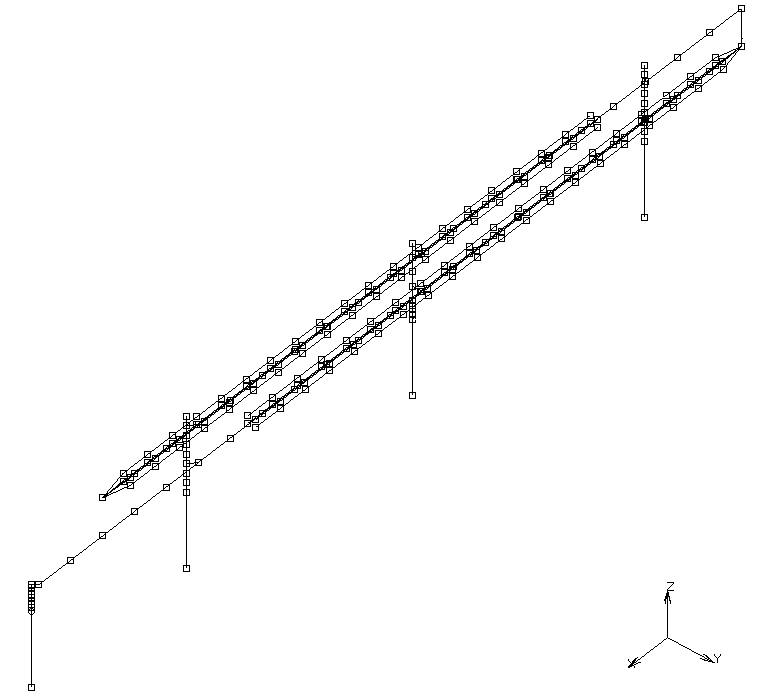
Abb. 2: FE-Netz für die
'verpackte' Antenne
Literatur
[1]
Stöcker, H.: Taschenbuch der Physik. Verlag Harri Deutsch, Frankfurt am
Main, 1994
Temperature distribution on the stowed and deployed antenna as a function of
solar angle and radial distance from the sun.
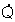 von den Supports zum Raumschiff den
Betrag von 2 W nicht überschreiten. Für die ‘verpackte’ Antenne
gilt eine weitere Spezifikation: Die Temperatur am Support 3 (50042) muß
bei einer Entfernung von einem AU im Bereich von -80 °C bis 100 °C
liegen. Von Interesse ist auch die Temperatur am Support 1 (50041) und die
Temperatur am Punkt, an dem sich der Dipol kreuzt.
von den Supports zum Raumschiff den
Betrag von 2 W nicht überschreiten. Für die ‘verpackte’ Antenne
gilt eine weitere Spezifikation: Die Temperatur am Support 3 (50042) muß
bei einer Entfernung von einem AU im Bereich von -80 °C bis 100 °C
liegen. Von Interesse ist auch die Temperatur am Support 1 (50041) und die
Temperatur am Punkt, an dem sich der Dipol kreuzt. der Einheitsvektor der
Strahlungsrichtung und
der Einheitsvektor der
Strahlungsrichtung und 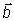 der
Orientierungsvektor der Struktur (siehe Abschnitt 2.1.2), dann ist der Anteil
f der einfallenden Strahlungsdichte
der
Orientierungsvektor der Struktur (siehe Abschnitt 2.1.2), dann ist der Anteil
f der einfallenden Strahlungsdichte
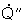 auf das Element:
auf das Element: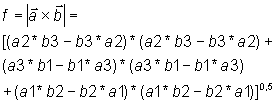 (1)
(1)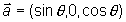 (2)
(2) (3)
(3)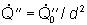 (4)
(4)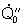 = 1344 W m-1 die Strahlungsdichte bei einem AU.
= 1344 W m-1 die Strahlungsdichte bei einem AU.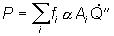 (5)
(5) (6)
(6)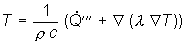 (7)
(7)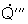 volumenbezogener Wärmestrom
an der Quelle/Senke, [W m-3]
volumenbezogener Wärmestrom
an der Quelle/Senke, [W m-3]  (8)
(8)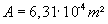 (9)
(9) (10)
(10)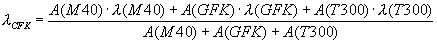 &#
9;
&#
9;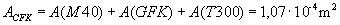 (12)
(12)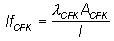 (13)
(13)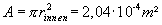 (15)
(15)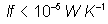 (16)
(16)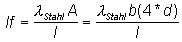 (17)
(17) (18)
(18)