|
MPAE-W-100-94-27
MAX-PLANCK-INSTITUT FÜR AERONOMIE
D-37191 Katlenburg-Lindau, Federal Republic of Germany
______________
The Tetrahedron Quality Factors of CSDS
1994 June 7
This report available from
http://www.mpae.gwdg.de/~daly/tetra.html |
|
The four Cluster spacecraft will form a tetrahedron, which ideally should be a regular
one: equal spacing between all pairs of vertices. In reality, this will not be the case. A number
of parameters exist to specify how badly off the true figure is. This paper presents some
mathematics of tetrahedrons, describes the two parameters that are to be used in the Cluster
Science Data System, and gives a Fortran program for their calculation. |
|
Introduction
The "Glassmeier" Parameter
The "Robert/Roux" Parameter
Mathematics of a Tetrahedron
Area of a Side
Volume of a Tetrahedron
Center of Circumscribed Sphere
The Regular Tetrahedron
Calculating the Quality Factors
Four points in space define a tetrahedron. If the
separations between each pair of points are equal,
then it is a regular tetrahedron. The four Cluster
spacecraft will form a tetrahedron, which in
general is not regular. How can we specify the
degree to which regularity is achieved?
| Table 1 | Special values of the Glassmeier
parameter |
| QG | Meaning
| | 1.0 | The four points are colinear |
| 2.0 | The points all lie in a plane |
| 3.0 | A regular tetrahedron is
formed |
| |
|
The parameter proposed by vom Stein, Glassmeier,
and Dunlop (1992) is defined as
and takes on values between 1 and 3. It tends to
describe the dimensionality of the figure, as listed
in Table 1. The ideal volume and surface are
calculated for a regular tetrahedron with a side
length equal to the average of the 6 distances
between the 4 points.
In their paper on tetrahedron shape, Robert and
Roux (1993) present 17 different parameters, as
ratios of various volumes, sizes, areas. Of these,
the CSDS community has decided to adopt one as
its second quality parameter for the auxiliary
data. It is defined as
where the sphere is that circumscribing the
tetrahedron (all four points on its surface) and 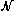 is a normalization factor to make QR = 1 for a
regular tetrahedron. The range of values is
between 0 and 1.
Consider four points in space and the figure
formed by joining them with lines (Figure 1). The
points are numbered 0 to 3, and their vectors are
r
0, r1, r2, r3. Without any loss of generality, we
may consider only the differences
is a normalization factor to make QR = 1 for a
regular tetrahedron. The range of values is
between 0 and 1.
Consider four points in space and the figure
formed by joining them with lines (Figure 1). The
points are numbered 0 to 3, and their vectors are
r
0, r1, r2, r3. Without any loss of generality, we
may consider only the differences
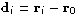
in describing the points.
|
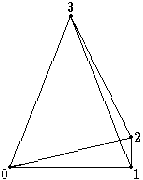
| Figure 1 | A tetrahedron and its four vertices. |
|
The area of a parallelogram bounded by two
vectors d1 and d2 is given by the magnitude of
their cross product; any triangle is half of a
parallelogram, so its area is
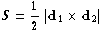
where d1 and d2 are the vectors for any two
sides of the triangle (Figure 2).
|
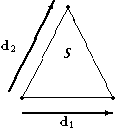
| Figure 2 | Area S of a triangle. |
|
For the four sides of the tetrahedron, specify
side n to be that one that does not contain point
n at any of its vertices. Thus:
| S1 | = | 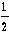 |d2 × d3| |d2 × d3| | | (3) |
|
| S2 | = | 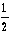 |d1 × d3| |d1 × d3| | | (4) |
|
| S3 | = | 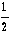 |d1 × d2| |d1 × d2| | | (5) |
|
| S0 | = | 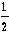 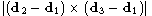 | | |
|
| = | 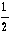 |d1×d2 + d2×d3 + d3×d1| |d1×d2 + d2×d3 + d3×d1| | | (6) |
The total surface S is the sum ċ
n=03Sn.
The volume of a figure bounded by three vectors
in space is the triple product of those vectors.
Any tetrahedron is 1/6 of such a figure, hence
| V | = | 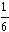 |d1 · d2 × d3| |d1 · d2 × d3| | | (7) |
|
| = | 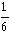 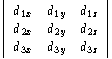 | | (8) |
To find the circumscribed sphere, we need the
point that is equidistant from all four vertices, i.e.
we want r such that | (r - rn) · (r - rn) | = | r2; "n = 0, 3 | | |
|
| r2 - 2r · r
n + rn2 | = | r2 | | |
If we take point 0 as the origin, that is, if we use
the dn vectors in place of the rn, then r2 = r2,
the sphere radius, and the above 4 equations
reduce to
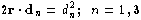
This yields the matrix equation for the center
of the sphere
which can be solved for the vector (x, y, z) and
the radius of the sphere r2 = x2 + y2 + z2. Note
that the leftmost matrix in equation 9 is the same
as the one whose determinant yields the volume
of the tetrahedron (equation 8).
The volume of the circumscribed sphere is then
The regular tetrahedron of unit side is the
ideal against which the true figure of the four
spacecraft is to be measured. We may take
| d0 | = | (0, 0, 0) | | |
|
| d1 | = | (1, 0, 0) | | |
|
| d2 | = | 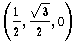 | | |
|
| d3 | = | 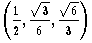 | | |
| Table 2 | Values for regular tetrahedron |
| Quantity | Value |
| S0 = | 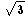 /4 /4 |
| S = | 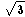 |
| V = | 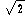 /12 /12 |
| r = | 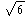 /4 /4 |
V  = = | 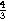 p p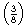 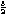 |
| = |
|
Values for the regular tetrahedron of unit side
length are listed in Table 2.
The quality factors in equations 1 and 2 can now
be found with the help of these formulas.
For QG, we average the 6 distances between the
4 points to get the side L of the "ideal" regular
tetrahedron, with volume L3 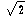 /12 and surface
L2
/12 and surface
L2 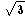 . The true volume and surface are found
from equations 7 and 3-6.
. The true volume and surface are found
from equations 7 and 3-6.
For QR, the radius of the circumscribing
sphere is calculated from equation 9. The actual
volume of the sphere need not be calculated, for
all the factors just go into the normalizing
 .
.
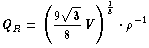
A Fortran program calculates both these
parameters.
|
|
| Robert, P. and Roux, A. (1993). Influence
of the Shape of the Tetrahedron on the
Accuracy of the Estimate of the Current
Density. Proceedings of ESA `START'
Conference, Aussois, France, Centre de
Recherches en Physique de l'Environment,
Issy les Moulineaux, France.
|
|
| vom Stein, R., Glassmeier, K.-H., and Dunlop,
M. (1992). A Configuration Parameter for
the Cluster Satellites. Tech. Rep. 2/1992,
Institut für Geophysik und Meteologie der
Technischen Universität Braunschweig.
|
/12 and surface
L2
. The true volume and surface are found
from equations 7 and 3-6.
.