Next: Earth magnetic pole
Up: Geocentric Systems
Previous: Geocentric Systems
The Greenwich mean sidereal time is defined by the hour angle
between the meridian of Greenwich and mean equinox of date at 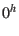 UT1:
[A. B6]:
UT1:
[A. B6]:
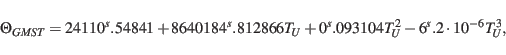 |
(18) |
in seconds of a day of 86400s UT1,
where 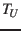 is the time difference in Julian centuries of Universal Time (UT1) from J2000.0.
is the time difference in Julian centuries of Universal Time (UT1) from J2000.0.
From this the hour angle in degree 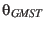 at any instant of time
at any instant of time 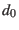 (Julian days from J2000.0)
can be calculated by
(Julian days from J2000.0)
can be calculated by
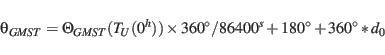 |
(19) |
For the precision needed in this paper we may neglect the difference between 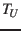 and
and 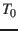 , such
that (Meeus, 2000):
, such
that (Meeus, 2000):
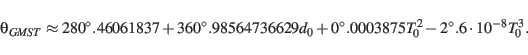 |
(20) |
Markus Fraenz
2017-03-13
![]() UT1:
[A. B6]:
UT1:
[A. B6]:
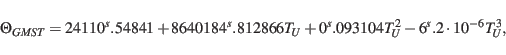
![]() at any instant of time
at any instant of time ![]() (Julian days from J2000.0)
can be calculated by
(Julian days from J2000.0)
can be calculated by