• Computational helioseismology
• Reynolds stress
• Pinsker estimator
• Noise estimation

Pinsker estimators in helioseismology

Using the Born approximation (single scattering approximation), the velocity depends linearly on the data (travel times). The forward operator is a convolution in the horizontal direction and the inverse problem can thus be solved efficiently in the Fourier space. The traditional methods used in helioseismology are the Regularized Least Square (RLS) or the Optimally Localized Averaging (OLA). However, for this kind of problem an optimal estimator among a given class of ellipsoid that minimizes the risk exists: the Pinsker estimator. This method yields significantly better reconstructions than traditional inversion methods used in helioseismology [1]. [1] Damien Fournier, Laurent Gizon, Martin Holzke, and Thorsten Hohage. "Pinsker estimators for local helioseismology: inversion of travel times for mass-conserving flows", Inverse Problems, 32(10), 105002 (2016).

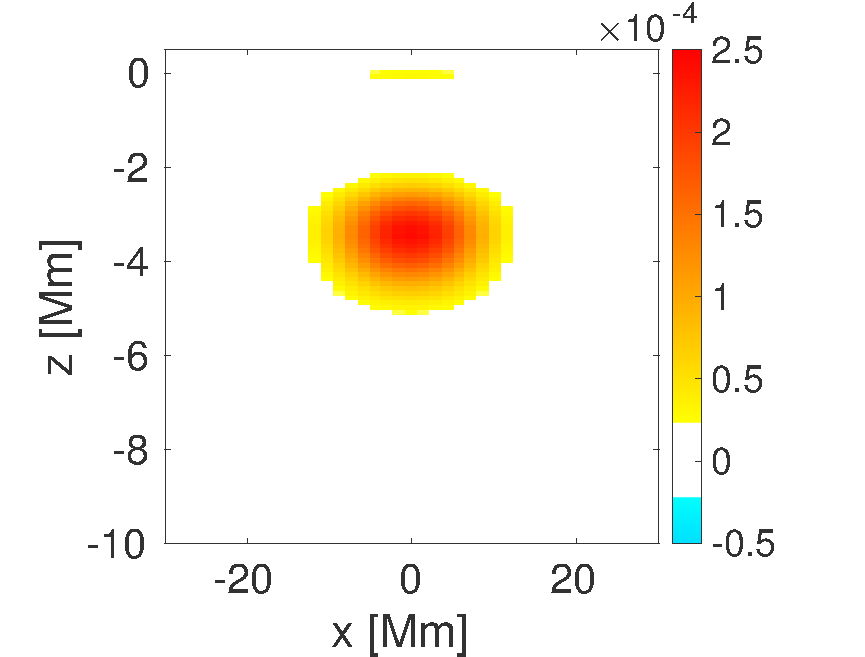
Averaging kernel at a depth of 3.5 Mm obtained by the Pinsker method which minimizes the risk of the linear estimator. This kernel peaks at the desired depth of 3.5 Mm which lead to a good reconstruction of the data.