Calculations

Here we outline the standard calculations involved to obtain the order of magnitude for the gravitational wave signal. Given two nearby test particles, such as those illustrated above in the animation, they will move in an oscillatory motion due to the influence of a passing gravitational wave.

The small change in the Newtonian gravitational potential ( $\delta\Phi$ ) comes readily by solving the equations of stellar pulsation. A Poisson equation arises for which the solution as presented by Cutler et. al. (1996) is

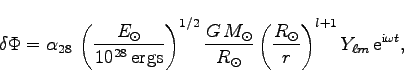$\begin{displaymath} \delta \Phi = \alpha _{28}\,\left( \frac {E_\odot}{10^{28}\,... ...frac {R_\odot} r\right)^{l+1} Y_{\ell m}\, \e^{\rmi \omega t}, \end{displaymath}$

(1)

where $\alpha _{28}$ is a normalisation factor. $E_\odot$ , $R_{\odot}$ , $M_\odot$ and

are respectively the solar energy, solar radius, solar mass and gravitational constant. The spherical harmonic has its standard definition $Y_{\ell m}$ and $\omega$ is the angular frequency of the passing gravitational wave. Thus for an $\ell=2$ mode, the perturbation to the potential falls off very quickly as $\frac 1{r^3}$ .

The relative acceleration between the two test particles arises from the Newtonian equation of deviation,

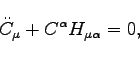$\begin{displaymath} \ddot{C}_\mu + C^\alpha H_{\mu \alpha } =0, \end{displaymath}$

(2)

where the Hessian has been defined $H_{\mu \nu } := \nabla _\mu \nabla _\nu \Phi$ . Here $C_\mu$ is a vector connecting the two test masses and a dot denotes differentiation with respect to time. Therefore, under a linear perturbation, it becomes

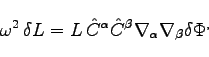$\begin{displaymath} \omega ^2\,\delta L =L\, \hat{C}^\alpha \hat{C}^\beta \nabla _\alpha \nabla _\beta \delta \Phi^, \end{displaymath}$

(3)

where $\hat{C}_\mu$ is a unit vector. Here,

is the unperturbed distance between the test particles and $\delta L$ is the small perturbation due to the perturbed Newtonian potential. Therefore, since the potential falls off as $\frac 1{r^3}$ for an $\ell=2$ mode, the strain $h := \frac{\delta L}L$ will fall off as $\frac 1 {r^5}$ .

This order of magnitude calculation holds true for the LISA design as the test masses will always be nearby with respect to the distance from the solar source. Whereas for ASTROD, the satellites will not always be nearby and thus an order of magnitude is anticipated to be lost. Therefore, any decrease in ASTROD's orbital radius design will have a significant improvement of imminent detection of both gravitational waves and solar g-modes.

The movie of the sun as shown above was taken from http://sohowww.nasa.gov/data/LATEST/current_eit_304.mpg

Page last updated on 1 January, 1970

Latest News

LISA: Click here for the latest information regarding the Laser Interferometer Space Antenna.

ASTROD: Click here for the latest news and developments for the Astodynamical Space Test of Relativity using Optical Devices.