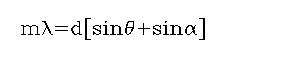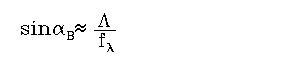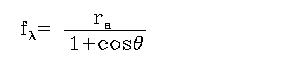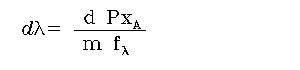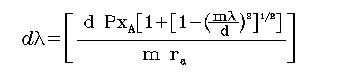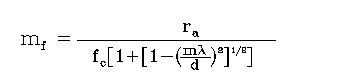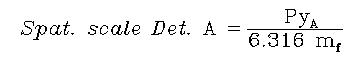Instrumentation and data reduction

·        1.1 The SUMER spectrograph

·        1.2 SUMER data reduction

o       1.2.1 Dead-time & local gain correction

o       1.2.2 Flat-field correction

o       1.2.3 Geometrical distortion

o       1.2.4 Radiometric calibration

o       1.2.5 Wavelength calibration

o       1.2.6 Additional corrections

§       1.2.6.1 Instrumental broadening

§       1.2.6.2 Slit magnification and displacement

§       1.2.6.3 Long- and short-period instrumental periodicities

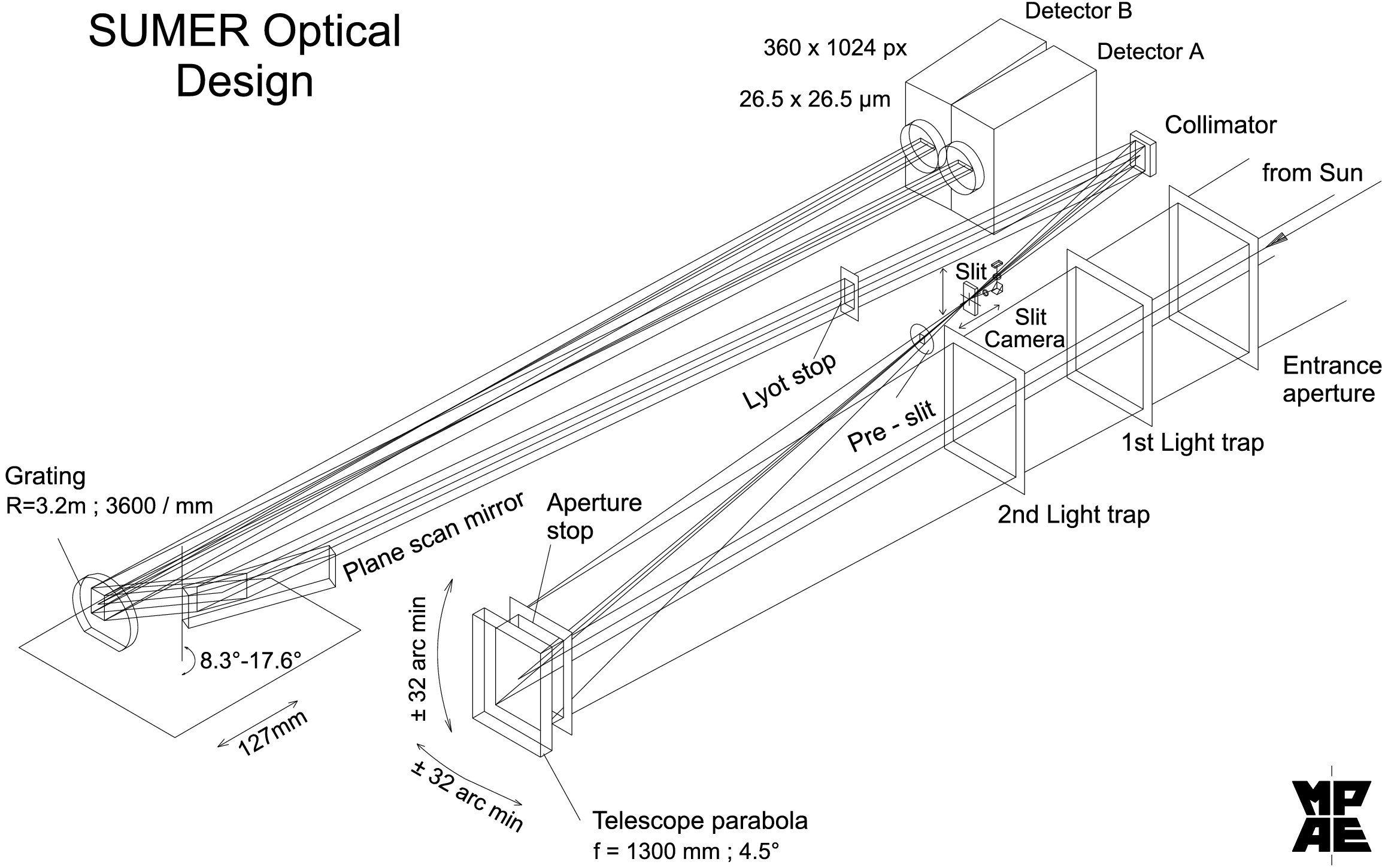
1.1 The SUMER spectrograph

SUMER is a powerful UV instrument capable of making reliable measurements of bulk motions in the chromosphere, TR and low corona with an accuracy better than 2 km s-1 (Wilhelm et al. 1997), with a spatial resolution of 1 arcsec (one arcsec at L1 corresponds to 715 km on the Sun) across the slit and 2 arcsec along the slit (Lemaire et al. 1997). The basic characteristics, capabilities and operations of SUMER are well described by Wilhelm et al. (1995, 1997) and Lemaire et al. (1997). The optical design (see Fig. 1.1) is based upon two parabolic mirrors, a plane mirror and a spherical concave grating, all made of silicon carbide (SiC). The first off-axis telescope parabola, which has pointing and scan capabilities, images the Sun on the spectrometer entrance slit. The second off-axis parabola collimates the beam leaving the slit. This beam is then deflected by the plane mirror onto the grating. Two detectors (called A and B), located in the focal plane of the concave grating, collect the monochromatic images of the spectrometer entrance slit. The centre of detector A is located on the grating normal, while the centre of the other detector is off by a quantity Delta = 70.4 mm. Coverage of the full spectral range of the instrument requires a wavelength scan performed by rotating the plane mirror. A baffle system, consisting of an entrance aperture, light traps, an aperture stop, a pre-slit and a Lyot stop, completes the design.

SUMER Optical Design

Figure 1.1: Optical layout of the SUMER instrument showing the light-path through the system. The ranges of movements of various mechanisms provided to control the position of the optical components are indicated by arrows. The entrance door and its mechanism are not shown. The spectrometer compartment is completely encapsulated in order to achieve good stray light performance and will only be illuminated through the slit engaged (from Wilhelm et al. 1995).

A brief summary of the basic SUMER optical characteristics is given in Table 1.1 below.

Table 1.1: SUMER optical characteristics (extracted from: Wilhelm et al. 1995, with up-to-date values).

Telescope:

&xnbsp;

 

&xnbsp;

Focal length

1302.77 mm at 75°C

 

Equivalent f-number

10.67

 

Plate scale in slit plane

6.316 µm arcsec-1

 

Smallest step sizes
(N-S and E-W)

0.3763 arcsec

&xnbsp;

 

Slits:

&xnbsp;

 

&xnbsp;

1

4.122 x 299.2 arcsec2

 

2

0.986 x 299.2 arcsec2

 

3

0.993 x119.6 arcsec2 (top)

 

4

0.993 x 119.6 arcsec2 (centered)

 

5

0.993 x 119.6 arcsec2 (bottom)

 

6

0.278 x 119.6 arcsec2 (top)

 

7

0.278 x 119.6 arcsec2 (centered)

 

8

0.278 x 119.6 arcsec2 (bottom)

 

9

1 arcsec ø

 

Spectrometer:

&xnbsp;

 

&xnbsp;

Wavelength ranges

 

Detector A

390 - 805 Å (2nd order)*

 

780 - 1610 Å (1st order)

 

Detector B

330 - 750 Å (2nd order)*

 

660 - 1500 Å (1st order)

 

Collimator focal length

399.60 mm

 

Grating radius

3200.78 mm

 

Grating spacing

2777.45 Å (3600.42 lines mm-1)

 

Detectors:

&xnbsp;

 

&xnbsp;

Array size

1024 (spectral) x 360 (spatial) pixels

 

Mean spectral pixel size

26.6 µm (Det. A); 26.5 µm (Det. B)

 

Mean spatial pixel size

26.5 µm (Det. A); 26.5 µm (Det. B)

 

* In the range below 500 Å the sensitivity is very low, because of three normal-incidence reflections. Strong lines have,
however, been observed in this regime during the calibration phase and under operational conditions.

The instrument can also provide monochromatic images (``Raster'') of selected areas of the Sun by rotating the primary mirror in the east-west direction of elementary steps of 0.3763 arcsec. The scanning capability can also be used to compensate for the solar rotation (Wilhelm et al. 1995). Since October 1996, problems with the azimuthal scan mechanism, had prevented the acquisition of raster scans. The raster mode has been once again available from February to November 1999. However, small areas near disk centre could still be scanned using the solar rotation (~10 arcsec in one hour at disk centre).

SUMER is equipped with two photon-counting detectors (A and B) with Cross Delay Line readout (XDL) technique (for details see Siegmund et al. 1994). However, only one detector can be operated at a time. Each detector has 1024 spectral pixels and 360 spatial pixels. When an exposure is taken, either the full (1024 pixels) spectrum or selected spectral windows (25, 50, 256 or 512 pixels wide) are transmitted to the ground. If the 1 x 120 or the 0.3 x 120 arcsec2 slit is used, it is possible to transmit only the illuminated horizontal band of the detector. The central area of the detectors is coated with a potassium bromide (KBr) layer which increases the detective quantum efficiency up to a factor ~ 20 in the range from 900 Å to 1600 Å (see Fig. 1.2). In the SUMER spectrograph the diffraction orders are superimposed. The rotation of the flat mirror allows the coverage of the spectral range between 780 and 1610 Å (detector A), thus recording also second order lines between 390 and 805 Å. However, the fall-off of the SiC reflectivity severely reduces the possibility to observe lines at wavelengths below 500 Å. Second order lines (400 - 800 Å) are largely insensitive to the KBr coating (see Fig. 1.4), allowing us to recognize the second order lines from the first order ones using the different wavelength-dependent sensitivity of KBr compared to the bare part. For this reason, when the entire wavelength range is scanned, every spectrum is partially overlapping the previous and the following, in order to ensure that the spectral lines are recorded on both the bare and the KBr parts of the detector.

SUMER raw UV quiet Sun spectrum around 1450 Å (detector A).

Figure 1.2: SUMER raw UV quiet Sun spectrum around 1450 Å obtained on 30 January 1996 at disk centre. The top panel shows the full area of detector A (1024 x 360 pixel2) imaged through the 1 x 300 arcsec2 slit. In this case only ~ 300 spatial pixels are illuminated. No correction has been applied to the spectrum. The different sensitivity of the KBr coating on the central part of the detector (from detector pixel 280 to 770 in the case of detector A) with respect to the bare part appears immediately evident. At this wavelength the difference in sensitivity is a factor of 10. The geometrical distortion of the image is also evident. The largest detector MCP defect can easily be seen around the pixel coordinates (575, 255). In the lower panel is shown the spectrum obtained averaging along the slit.

1.2 SUMER data reduction

SUMER data from the original telemetry are available in two different forms: FITS and IDL-restore files, both produced from GSFC-generated CD-ROMs. The quality will ultimately be the same, but differences exist in the structure of files and the header information. The IDL-restore files contain all of the instrument housekeeping and science data. The FITS data are stored in the SOHO archive at GSFC and the remote sites of the archive, while the IDL-restore files can be produced at MPAe (in Germany) where all SUMER-related CD-ROM data are stored on disk as binary files which are accessible by a Quicklook programme. This allows a quick inspection of a data set before converting the data into restore files. - Since May 2001, the MPAe computer centre has set up a web-based system (SUMER Image Database) which allows to browse through and download SUMER images.

Reduction of SUMER raw images follows several stages, i.e. decompression and reversion (for IDL-restore files), dead-time correction, local gain correction, flat-field correction, a correction for geometrical distortion and radiometric calibration (in order to pass from count px-1 s-1 to Watt m-2 sr-1 Å-1; and to correct for the differences in sensitivity between the KBr and the bare microchannel plate). Some other corrections can also be important in particular cases.

A step-by-step description of the routines used for the reduction of SUMER IDL-restore files can be found in the Data Corrections Cookbook.

In the case of SUMER FITS files a unique routine (calling all the necessary ones) has been written by K. Bocchialini and P. Lemaire. Further information can be found at the MEDOC site.

1.2.1 Dead-time & local gain correction

For a total counting rate greater than 5 x 104 event s-1, a correction for the electronic dead-time effect needs to be applied (Wilhelm et al. 1995; Hollandt et al. 1996). It is important to bear in mind that, whether or not only a part of the detector (sub-format image) is telemetered to the ground, the full detector area has been exposed. Thus, the total count rate on the detector cannot be inferred from the total counts in an image if sub-format images are used. In the last case the XEVENT and YEVENT parameters, that can be obtained from the header of the IDL-restore files (not the FITS or FTS header), needs to be used. Alternatively, if the full spectral image is also available (such an exposure is generally taken in the course of a sequence), it is possible to evaluate the ratio between the counts in the area corresponding to the sub-format image and the counts in the full detector frame. In this case the full detector count rate for each sub-format image can be estimated dividing the total counts in the sub-format image for the above ratio.

Another important effect arises when, for certain bright lines (i.e. C III 977 Å or O VI 1032 Å), levels around 10 counts pix-1 s-1 or higher are reached. In these cases a local reduction in the micro-channel plate (MCP) gain and, therefore, a loss of dynamic range will be present for such strong lines (Wilhelm et al. 1997). In addition, long exposures of such bright lines at the same pixel position on the detector will lead to a local reduction in the gain after a certain amount of total counts (total charge) has been extracted. 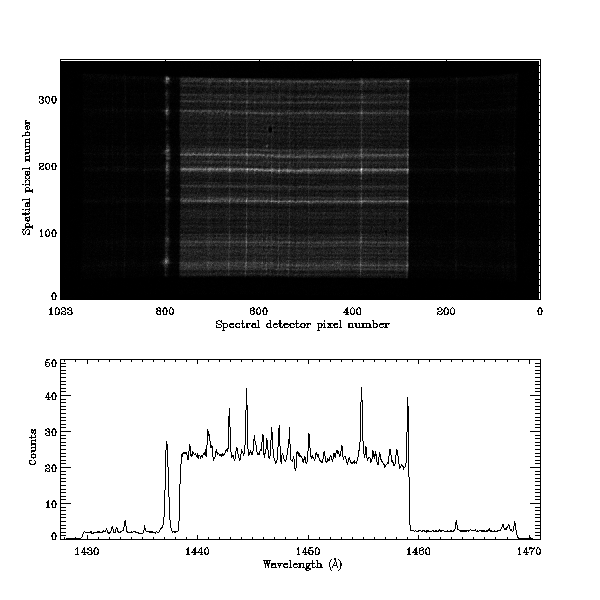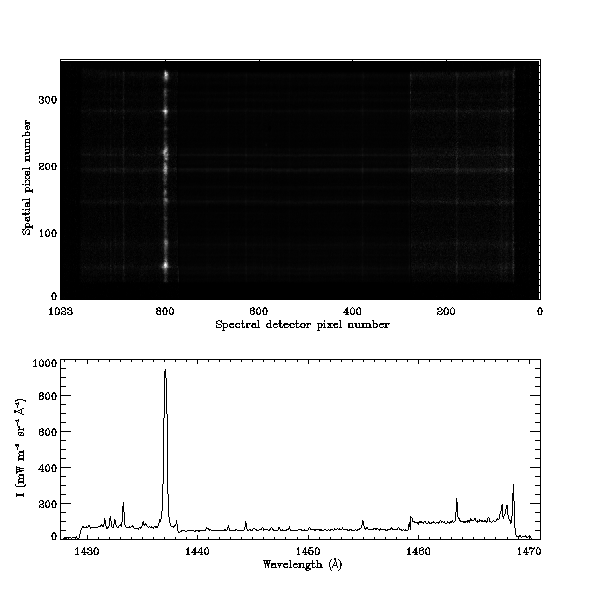An example of the last effect occurred after the full Sun scan in C III 977 Å on 28 January 1996 which left an imprint of reduced gain around detector (A) pixel 848 (see Fig. 1.2). In these cases also a correction for the local gain depression needs to be applied at the initial stage. Local gain correction requires dead-time correction to be applied first.

Note that in cases of particularly high local count-rates the line can produce a ghost around ~2.2 Å towards higher wavelenghts (see section 2.2.4).

1.2.2 Flat-field correction

Flat-field correction is necessary in order to correct for non-uniformities in the sensitivity of the detector on scales of about 20 pixels or less. These are mostly due to a non-linearity of the A/D-converters and the hexagonal pattern of microfiber bundles of the MCPs. Flat-field images are taken approximatively every month with a ~ 3 hour exposure in the Lyman continuum between 860 and 900 Å while the spectrometer grating is de-focused (Schühle et al. 2000). In some cases the flat-field correction is performed on board using the last acquired image. The flat-field correction also eliminates or, at least greatly reduces, a modulation of approximatively 19 % every two pixels in the spatial dimension caused by an analogue-to-digital converter differential non-linearity (Siegmund et al. 1994). 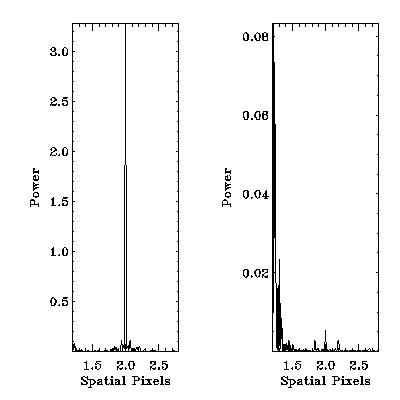This gives us the possibility to verify whether an image was flat-field corrected or not, simply by comparing a power spectrum of the averaged image along the slit before and after the flat-field correction (Teriaca et al. 1999). The disappearance of the peak at period 2 is a clear signature that the flat-field correction has been applied. However, in order to apply this technique, it is important that the spectrum in question is characterized by a sufficiently high signal-to-noise ratio. In Fig. 1.3 the Fourier analysis for the quiet Sun spectrum shown in Fig. 1.2, before and after the correction with a flat-field taken on 2 February 1996, is presented.

Carlsson, Judge and Wilhelm (1997) found a drift in the fixed pattern of the detector with time, which is caused by scrubbing by the electrons extracted in the channel plates (Griffiths et al. 1998). It is thus a function of the total charge extracted from the channel plates. Since this depends on the location where bright spectral lines have been registered on the active detector area, this is not uniform in time and spatial location. It leads to a non-uniform drift of the fixed pattern, except the 19 % pixel-to-pixel variation which is induced by the digitisation. It is thus completely independent of the channel plate usage and is not moved by this effect (Schühle, private communication). This drift can only roughly be interpolated between subsequent flat-field exposures. In this way only a temporal and spatial average of the drift can be determined. Since the 19 % pixel-to-pixel variation, induced by the ADC, is a pattern that is not shifted, it has to be corrected separatly, before a shifted flat-field correction is applied. For this purpose, the SUMER calibration data base provides an image (for A and B detector each) that can be applied to the data by using the flat-field correction routine. This will remove the odd-even row pattern from the data by multiplication of an ODD_EVEN_ARRAY. Of course, in this case, flat-fields with the odd-even pattern removed must be used.

In general, when the data and the closest flat-field are only few days apart, the drift should be small. Teriaca et al. (1999) found a drift of 0.037 pixels (in the spectral direction) between data and a flat-field ~3 days apart. This corresponds to approx. 0.4 km s-1 at 1250 Å. Such a drift is, however, much smaller then the residual errors in the geometrical distortion correction (see below) and can be ignored. However, attention must be paied when the data and the closest available flat-field are many days apart.

In the case of some particular observations (e.g. large rasters of the quiet Sun) a technique to extract the flat-field matrix directly from the data has been described by Dammasch et al. (1999).

Power spectrum of the average along the slit before and after the flat-field subtraction.

Figure 1.3: Power spectrum of the average along the slit of the Quiet Sun detector image showed in Fig. 1.2, before (left) and after (right) the flat-field correction, showing the reduction in the electronic modulation (see Teriaca et al. 1999, for another example).

1.2.3 Geometrical distortion

The electronic design of the detector induces a geometrical distortion of the images produced by SUMER in an ``inverse cushion'' fashion that is most evident at the extremities of the image. This effect can be corrected using different routines all based on DESTR_BILIN.PRO that uses rectangular grid tables obtained through spatially averaged spectra of narrow O I lines by T. Moran (2002). However, residual errors remain close to the extremes of the slit (see Fig. 1.5). Peter (1999a), Peter & Judge (1999) and Judge et al. (1998) stress that the geometrical correction routine leaves a residual wavelength error that has a maximum value of ~ 0.2 pixel. As described in the previous paragraph (flat-field correction), the image has shifted with time as the detector has been used (extracted charge). The geometric distortion correction cannot account for this shift: which leaves a residual error in the geometric image correction. It can be adopted an error of 0.15 pixel taking into account these residual effects. This corresponds to an error of ~ 1.5 km s-1 around 1250 Å.

1.2.4 Radiometric calibration

The radiometric calibration of the SUMER spectrograph was performed in the laboratory using a secondary source standard, traceable to the Berlin Electron Storage ring for SYnchrotron radiation BESSY I (Hollandt et al. 1996). During previous UV space missions, serious losses in sensitivity were observed during the operational life (OSO-6: Huber et al. 1973; ATM Reeves et al. 1977; OSO-8: Lemaire et al. 1991). The degradation is due to the outgassing of organic substances from materials employed in the construction and their subsequent deposition on irradiated surfaces (Steward et al. 1989). In order to reduce possible sources of contamination, a very strict cleanliness program was carried out through all the phases of development of the mission. The stabilities of both detectors has been monitored since the beginning of the operational phase. Results of the first 15 months demonstrate that there was no in-flight degradation experienced (Schühle et al. 1998). This monitoring has continued until the present time and no degradation was detected before the loss of attitude of SoHO in June 1998. Thereafter, a loss of responsivity of 43 % (on average) has occurred (Wilhelm et al. 2000; Schühle et al. 2003).

In-flight calibration curves were obtained through an iterative process leading to a continual improvement in the final result. Calibration curves were first refined in flight for both orders and for both photocathodes with the help of star data and line ratio methods (Wilhelm et al. 1997). These results have been compared with data from other UV instruments, and particularly from SOLSTICE (Woods et al. 1998). After the comparison (Wilhelm et al. 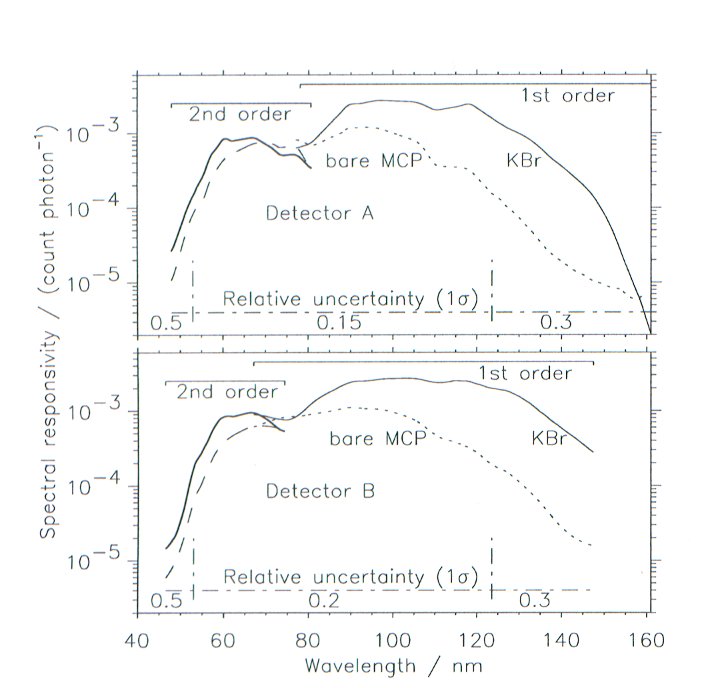1999), responsivity curves were revised and are now available for the KBr photocathode and the bare MCP, respectively (see Fig. 1.4). Uncertainties for detector A are estimated to be 15 % from 540 to 1205 Å, 30 % above 1250 Å on KBr. Below 540 Å only very few lines can be observed, and the data need further confirmation. At this stage the uncertainty is estimated to 50 % (1 sigma) (Wilhelm et al. 2000). The KBr data for detector A in this range need further study. In order to increase the life-time of detector B, in September 1996 it was decided to operate it at a lower gain than during the calibration phase in laboratory. This led to larger uncertainties in the responsivity curves. Uncertainty below 540 Å remains as high as 50 %. In the main part of the spectral range, from 540 Å to 1236 Å, the uncertainty is below 20 % (Schühle et al. 2000). The radiometric calibration is performed through the provided software (RADIOMETRY.PRO, written by K. Wilhelm). Responsivity curves are subjected to continuous study and can be changed from time to time. Hence, it is very important to make sure that the latest calibration is used.

Spectral responsivity curves for SUMER detectors A and B.

Figure 1.4: Spectral responsivity curves for SUMER detectors A and B, together with the corresponding relative uncertainties for the 1 x 300 arcsec2 slit. Above 1250 Å the relative uncertainty relates only to the KBr part of the detectors. The uncertainties shown in the above diagram include the contribution of optical stops and diffraction effects, but the pixel size uncertainty has to be treated separately. In the central wavelength range, detector B shows larger uncertainties due to the lower gain at which the system is operated. Be aware that responsivity curves are updated from time to time and the latest curves should always be used.

SUMER reduced UV quiet Sun spectrum around 1450 Å (detector A).

Figure 1.5: SUMER corrected and calibrated UV quiet Sun spectrum around 1450 Å obtained on 30 January 1996 at disk centre. The top panel shows the full area of detector A (1024 x 360 pixel-2) imaged through the 1 x 300 arcsec2 slit. In this case only ~ 300 spatial pixels are illuminated. Dead-time and local gain corrections, flat-field, radiometric calibration and correction for geometrical distortion has been applied to the spectrum (compare with the raw spectrum in Fig. 1.2. In the lower panel is shown the spectrum obtained averaging along the slit.

1.2.5 Wavelength calibration

Particular attention needs to be paid to the problem of the wavelength calibration. In the case of SUMER, there is no calibration source aboard, so the wavelength calibration is done using some chromospheric lines of neutral atoms. These lines are formed in the chromosphere at temperatures around 6500 K (e.g. Si I and S I, Chae et al. 1998a) and are supposed to be at rest (Samain 1991). These lines should therefore allow the determination of an absolute wavelength scale. Lines such as C I, O I and Fe II are formed at temperatures higher than S I and Si I, (Chae et al. 1998a) and can present a certain amount of Doppler shift. Chae et al. (1998a) found redshifts of 1.5, 1.8 and 1.8 km s-1 for C I, O I and Fe II, respectively. Hassler et al. (1991), using the LASP EUV Coronal spectrometer on a sounding rocket flight, found a redshift of 2.7 km s-1 for Fe II 1563.790 Å. Thus, this amount of Doppler shift should be taken into account before using these lines as zero-point reference. It is important to remember that all the absolute velocity measurements made with SUMER will be relative to those chromospheric reference lines. This also means that, whenever absolute velocity measurements are required, the full spectral detector range (or, at least, half of it) needs to be available in order to have enough reference lines to obtain a reliable wavelength scale. In several cases this is not possible and only velocities relative to average values will be obtained. Chromospheric lines disappear below 900 Å, reducing the wavelength range in which it is possible to make an absolute measure of velocity, to 900 - 1600 Å. However, due to the superposition of the orders, some strong second order lines are recorded against the first order chromospheric lines, thus allowing the precise measure of the central wavelength of important lines such as, e. g., Ne VIII 770.428 (Dammasch et al. 1999). In Fig. 1.6 we have an example of a quiet Sun SUMER spectrum recorded around 1400 Å. It is possible to see some second order lines overlapping the first order ones as well as chromospheric lines that can be used for wavelength calibration.

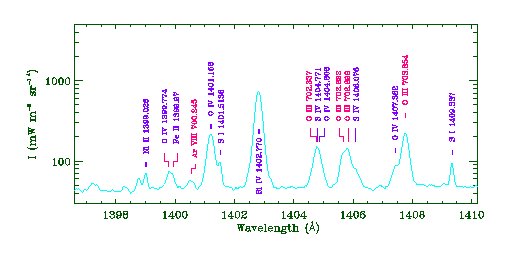
July 10 1996 SUMER reference spectrum of the quiet Sun around 1400 Å

Figure 1.6: SUMER spectrum of the quiet Sun around 1400 Å. The spectrum has been obtained averaging along the slit a full detector exposure obtained on 10 July 1996. Note the lines from both first and second order present in this spectral range and, particularly, the ones belonging to the O IV 1400 Å multiplet and, superposed, a group of second order O III lines.

A careful measurement of the absolute line position of several spectral lines across the SUMER spectrum was carried out by Teriaca et al. (1999) for two datasets relative to the quiet Sun and to the active region NOAA 7946. In this case almost the entire spectral range between 800 and 1600 Å was covered in several full spectra recorded with detector A.

A preliminary wavelength scale was found for every spectrum using the information contained in the data header (wavelength of reference pixel). In fact, considering the grating equation, we have:

Eq. 1

[1]

where m is the diffraction order, d is the grating spacing, the angle of incidence on the grating and the angle of reflection off the grating. In the case of detector A, sin () =0 while for detector B we have:

Eq. 2

[2]

where is the distance between the centres of the two detectors. For a spherical concave grating of radius ra (= 3200.78 mm), the effective focal length is given by:

Eq. 3

[3]

Consider the case of detector A, cos ()=1. Differentiating Eq.1 with kept constant and assuming f / d = dx (where dx is the scale of the resolution, given by the pixel size in the spectral direction), we obtain:

Eq. 4

[4]

where PxA is the spectral size of the pixels in detector A (26.6 µm, see Table 1.1). The dispersion value in the header of FITS files results from the above equation. Combining Eq.1, Eq.3 and Eq.4, we can write the dispersion as a function of the wavelength for detector A,

Eq. 5

[5]

The above equation can be used to build-up a preliminary dispersion relation, which is used as a starting point for the identification of the chromospheric spectral lines present in the spectra. Lists of lines observed on the Sun (on disk and off disk) are available in the literature (Curdt et al. 1997a, 2001; Kink et al. 1997; Feldman et al. 1997; Sandlin et al. 1986; Noyes et al. 1985; Cohen et al. 1978; Vernazza & Reeves 1978; Behring et al. 1976). For laboratory wavelengths of UV spectral lines, a large dataset can be found in the literature (Kelly 1982, 1985, 1987) and on the Internet (, e.g., Harvard-Smithsonian Center for Astrophysics Databases and the National Institute of Standard and Technology on-line energy level database).

After having identified as many chromospheric lines as possible, a Gaussian fit was applied to each one in order to derive its central position (in pixels). For each region of interest the dispersion relation was, hence, calculated performing a first order polynomial fit to the pairs `central pixel'-`laboratory wavelength' of the reference lines. This allows us to determine an absolute wavelength scale, making it possible to measure the central wavelength of all the other spectral lines. The use of a first order fit implies the assumption that the dispersion relation is locally linear. This assumption can be defended observing that the theoretical dispersion obtained from Eq.5 (see also Fig. 1.7) shows a small dependence on the wavelength, so that it can be considered constant in intervals of ~20 Å. 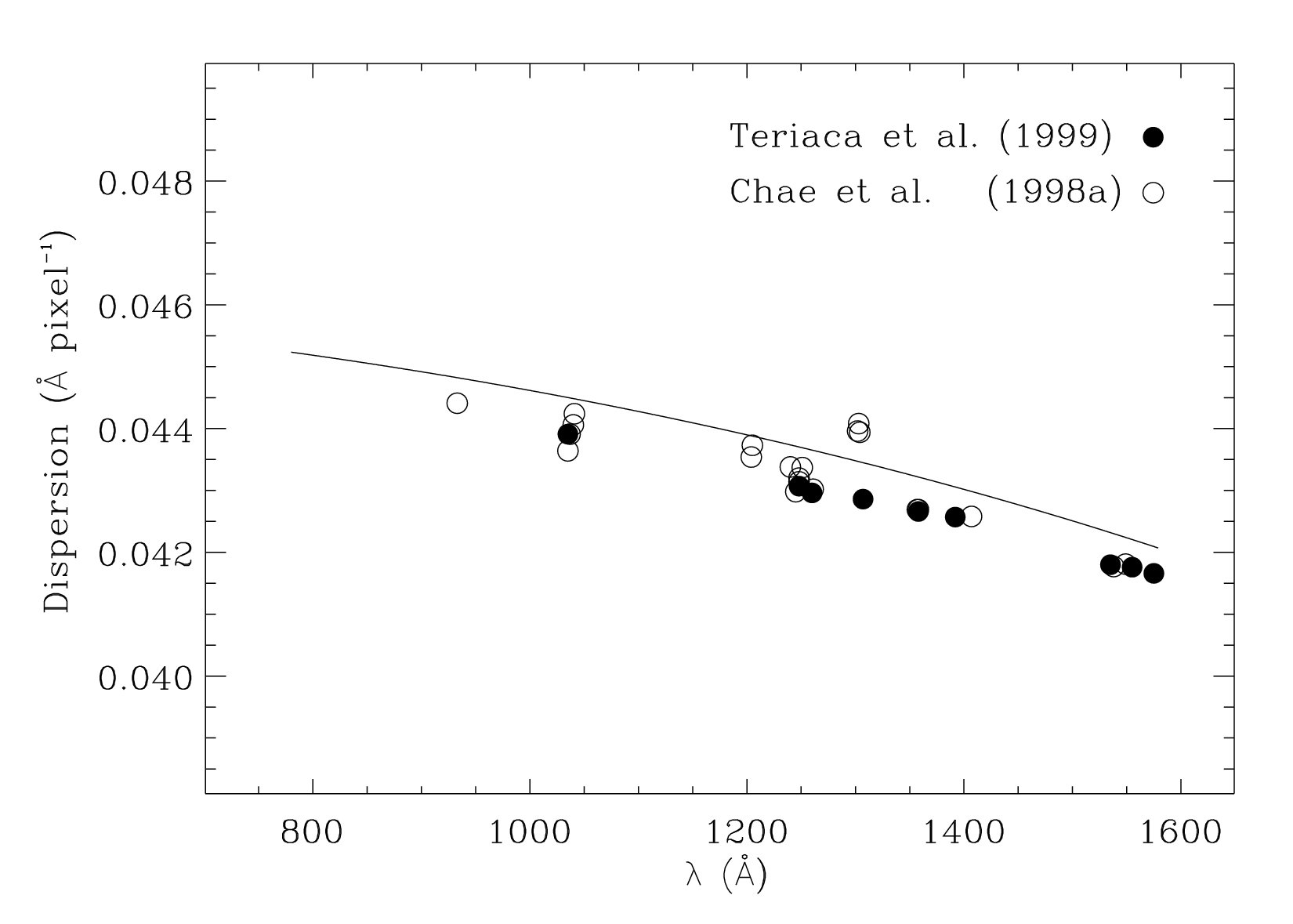The derived dispersion values are reported in Table 1.2. In Fig. 1.7 the dispersion values reported in Table 1.2 are shown together with the results obtained by Chae et al. (1998a) and with the theoretical trend from Eq.5. It can be noted how both the results from Teriaca et al. (1999) and Chae et al. (1998a) are slightly lower than the values obtained through Eq.5. Generally the laboratory wavelengths of chromospheric lines are well known, with errors much smaller than 1 km s-1.

Table 1.2: Dispersion values for different spectral regions as measured in the Quiet Sun and in Active Region NOAA 7946. Wavelengths for Iron lines are taken from Kelly (1985), all the others from Kelly (1982). In the first column, together with the spectral range, are also listed some of the ionic lines present in that range.

Spectral Range (Å)

Ref. line

Disp. (Å/pix)

1560 - 1590 (AR)


S V
O IV

Fe II 1563.790

0.04166

Fe II 1569.674

Fe II 1570.244

Fe II 1571.137

Fe II 1581.270

Fe II 1584.952

Fe II 1588.290

1540 - 1570 (AR)


C IV

Fe II 1550.274

0.04176

Fe II 1559.085

Fe II 1563.790

Fe II 1569.674

Fe II 1570.244

1520 - 1550 (QS)

Ne VIII

Si II 1526.7076

0.04180

Si II 1533.4320

C I 1542.1766

1380 - 1405 (AR)

O IV
Si IV
Ar VIII

Fe II 1387.219

0.04257

Fe II 1392.149

S I 1392.5878

Fe II 1392.817

S I 1401.5136

1350 - 1365 (AR)



Na IX
O I

C I 1354.288

0.04266

C I 1355.844

C I 1357.134

C I 1357.659

C I 1358.188

C I 1359.275

C I 1359.438

C I 1364.164

1295 - 1320 (AR)


Si II
Si III

S I 1295.6526

0.04286

S I 1300.907

C I 1310.637

C I 1311.363

C I 1311.924

C I 1312.247

1250 - 1270 (AR)

O V

C I 1254.513

0.04296

Si I 1258.795

S I 1262.8596

S I 1270.7821

1240 - 1255 (AR)


N V
Fe XII

C I 1244.535

0.04307

C I 1245.943

C I 1249.004

C I 1249.405

C I 1252.208

C I 1254.513

1025 - 1045 (QS)


C II
O VI

O I 1027.4307

0.04391

O I 1028.1571

O I 1039.2304

O I 1040.9425

O I 1041.6876

Spectral dispersion for detector A: theoretical and observational results.

Figure 1.7: Spectral dispersion for detector A: theoretical and observational results. The solid line represents the theoretical dispersion values for Detector A as obtained through Eq.5. Dispersion values obtained using chromospheric lines are also shown. Results represented by filled circles are from Teriaca et al. (1999), while open circles indicate values obtained by Chae et al. (1998a).

1.2.6 Additional corrections

After having applied all the above corrections, the spectra are ready to be analyzed. However, there are some other corrections that are important to apply in particular cases.

1.2.6.1 Instrumental broadening

This is a problem common to any spectroscopic analysis and concerns the fact that recorded line profiles are the result of the convolution of the instrumental profile with the true flux spectrum (Gray 1992). Emission lines arising from optically thin transition region and coronal plasma can be considered Gaussian in shape to a very good approximation (Mariska 1992). This is not strictly true for the instrumental profile. This implies that, in theory, the recorded spectral profiles should be not Gaussian in shape leading to the necessity of deconvolution processes of the data in order to extract the ``true'' spectrum. This is not a trivial operation with complications coming from the almost unavoidable presence of noise, data sampling and windowing (Gray 1992). Moreover, in order to perform the reconstruction process we should have the instrumental profiles for all the possible detector-grating angle-slit combinations. These profiles can be obtained in laboratory before the launch, but not during the flight (there are no calibration lamps aboard). However, in the large majority of cases (outside dynamic events and for lines formed in an optically thin plasma), SUMER line profiles can be fitted reasonably well by a single Gaussian. This demonstrates that the deformations in the observed line shapes induced by the instrumental profiles are indeed not important. This allows us to greatly simplify the problem by correcting only the measured full width at half maximum (FWHM). Tables of deconvolved values have been obtained for the different slits at different wavelength for both detectors. It is, hence, possible to correct the measured FWHM for the contribution of the instrumental profile using the provided software CON_WIDTH_FUNCT_3.PRO. Chae et al. (1998b) applied a Gaussian fitting technique to several Pt lines that were emitted by a hollow cathode source and recorded with detector A before launch, finding a FWHM of 1.95 pixels that do not show any significant dependence on the line wavelength. The same authors have also verified that the instrumental broadening has not deviated from laboratory values during the operational life of the instrument (at least not until August 1996). In Fig. 1.8, the ratio between the observed FWHM (FWHMobs) and the corrected one (FWHMsun) is shown for both detectors as a function of FWHMobs. It is evident how the importance of the correction decreases for the wider lines (FWHMobs > 300 mÅ).

Ratio between the observed FWHM and the corrected FWHM for both detectors

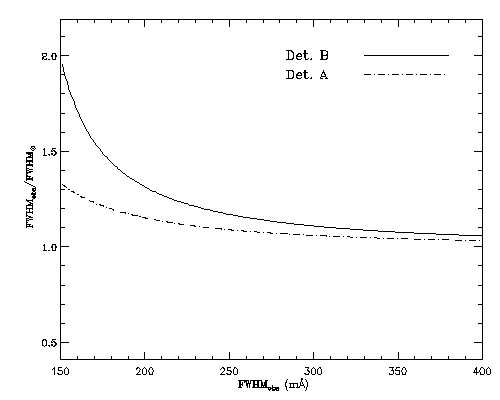
Figure 1.8: The ratio between the observed FWHM (FWHMobs) and the corrected one (FWHMsun) is shown for both detectors as a function of FWHMobs.

1.2.6.2 Slit magnification and displacement

The existence of a discrepancy between the orientation of the grating and the detector, causes the spectrum to be inclined with respect to the detector horizontal lines. This leads to a change in the vertical position of the slit image on the detector plane as a function of wavelength. Moreover, the position of the slit image on the detector is also shifted due to the nonlinearity of the grating focus mechanism which is moved simultaneously with the wavelength scan. And, last but not least, there may be a residual angle between the scan mirror rotation axis and the detector vertical lines, which may contribute to the displacement of the slit image.

Besides the displacement of the whole slit image, its projected size on the detector plane is also wavelength dependent. The scale of the Sun image focused by the primary mirror on the slit plane is 6.316 µm arcsec-1. This leads the long (1.89 mm) slit to cover 299.2 arcsec while the short (0.755 mm) slit will cover 119.6 arcsec (see Table 1.1). The slit is then projected by the collimator over the grating, which will finally focus monochromatic images of the slit onto the detectors (see Fig. 1.1). The final size of the slit image on the detector plane is determined by the ratio between the grating effective focal length f and the collimator focal length fc, the so-called magnification factor. In the case of detector A (sin()=0), combining Eq.1 and Eq.5 we can easily obtain the magnification factor mf as a function of wavelength,

Eq. 6

[6]

Using the value obtained from Eq.6, we finally obtain the spatial scale of the image on the plane of detector A as:

Eq. 7

[7]

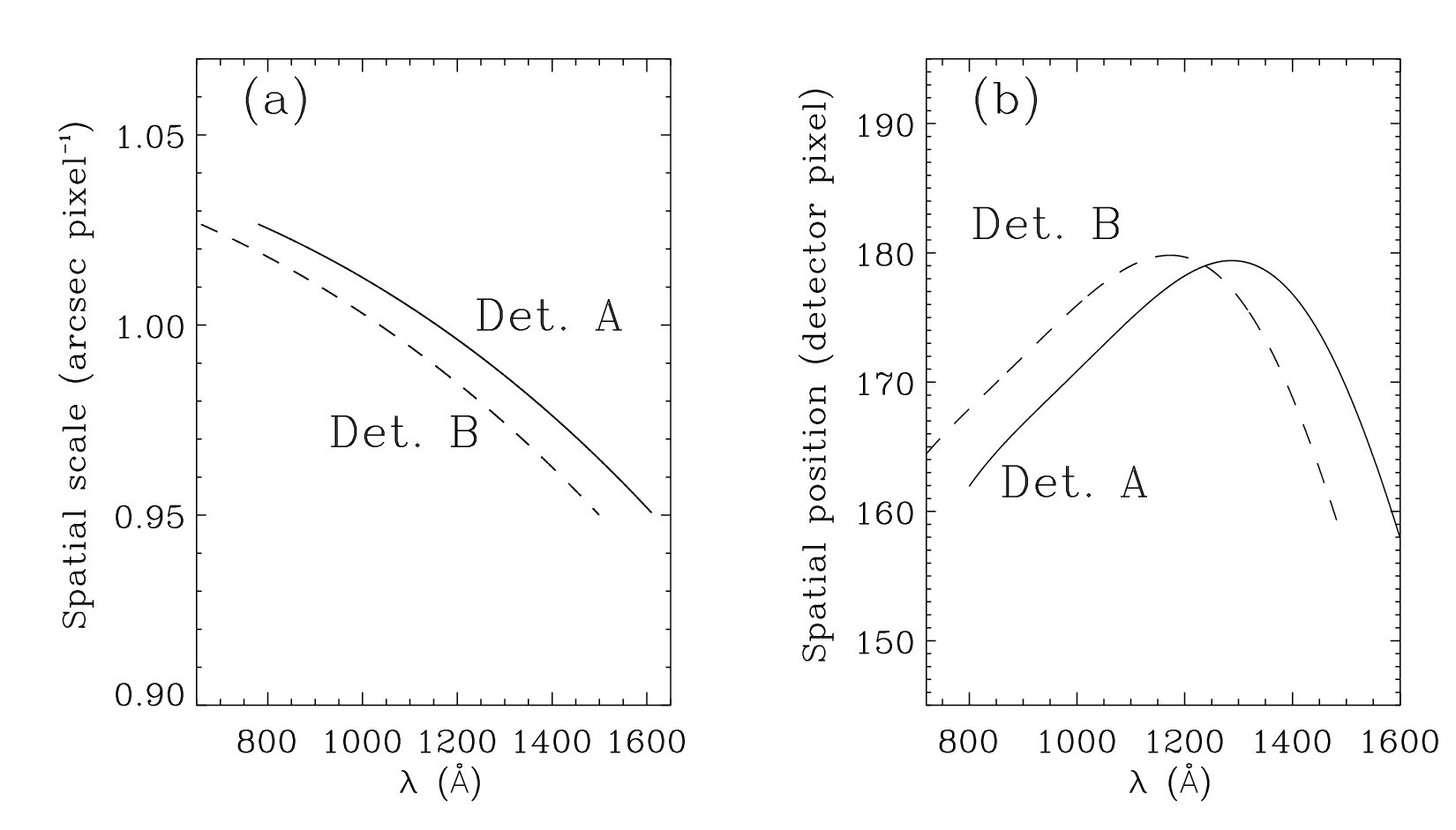
where PyA is the spatial size of the detector pixels (26.5 µm, see Table 1.1). From the last equation it is easy to calculate that the long slit will cover 291 and 315 spatial pixels of detector A at 800 Å and 1600 Å respectively. In Fig. 1.9a, the spatial scale of the slit image on the detector planes are shown as a function of the wavelength for both detectors.

The combined effects of the slit image displacement and magnification translate into the fact that, as an example, a solar feature recorded on detector A spatial pixel 179 at 1238 Å (N V) will be recorded around pixel 164 when observed at 1548 Å (C IV). The amount of displacement can be as high as 21 spatial pixels, corresponding to ~ 15000 km on the Sun surface. In Fig. 1.9b the spatial position (in detector pixels) of a point of the slit image falling on detector pixel 179 at 1238 Å, is shown as a function of wavelength for both detectors. The above correction needs to be applied only when comparing images obtained at different wavelengths. The vertical displacement and spatial scale of the slit image as a function of wavelength can be determined using the provided software (DELTA_PIXEL.PRO and MAGNIFICATION.PRO, respectively).

Slit image scale and spatial displacement on the detector planes as a function of wavelength.

Figure 1.9: Slit image scale and spatial displacement on the detector planes as a function of wavelength. (a): Image spatial scale as function of wavelength on detectors A (solid line) and B (dashed line). (b): Spatial position (in detector pixels) of a point of the slit image, falling on detector pixel 179 at 1238 Å, as a function of wavelength in the cases of detector A (solid line) and B (dashed line).

1.2.6.3 Long- and short-time instrumental periodicities

Despite the very high thermal and mechanical stability characterizing the instrument (the temperature inside the spectrometer compartment being controlled to within ± 0.15 K, Wilhelm et al. 1997), a drift of the whole spectral image has been detected by Curdt et al. (1997b). This periodic drift is due to thermoelastic oscillations. It was later found also by Dammasch et al. (1999), Peter (1999a, 1999b), Muglach & Fleck (1999) and Rybák et al. (1999a). In all these cases, the authors report a periodic drift with an amplitude up to 1 pixel and a periodicity of 1-2 hours. We interpreted these oscillations as the effect of mechanical deformations of the spectrometer structure due to small temperature changes induced by the spectrometer heaters. The drift can be avoided by switching off the heaters during the observational sequence (W. Curdt, personal communication). The problem appears whenever a sequence involves a considerable amount of time. This is true in the case of temporal series (i.e. sequences of spectra obtained keeping the slit fixed over the same point on the solar surface) devoted to the study of solar chromospheric, transition region and coronal oscillations as well as in raster scans (the slit is moved to an adjacent position after each exposure) of large areas of the solar surface. The drift can assessed looking at the behaviour of the mean line position averaged over all the individual line positions along the slit. In fact, the average along the slit greatly reduces the variations of solar origin, and the large scale variations of the mean position through the dataset will underline the presence of the instrumental drift. A spline fit, or a smoothing procedure, can be applied to the mean line position in order to remove residual variations of solar origin, obtaining a good estimation of the large-scale instrumental drift (see Fig. 2 in Peter 1999a and discussion therein). The drift so obtained can hence be subtracted. Of course, the determination of the drift is more accurate when it can be obtained averaging the results of various lines.

A possible problem also exists for temporal series during which a compensation for the solar rotation is applied (Rybák et al. 1999b). These authors suggest that the stepping mechanism could introduce spurious frequencies in the power spectrum of solar oscillations. In the case of temporal series obtained without compensation for the solar rotation there is no problem of introducing short-period variations, but attention has to be paid to the fact that features drift across the strip of solar surface imaged by the slit.

Luca Teriaca, teriaca@mps.mpg.de
Udo Schühle, schuehle@mps.mpg.de
Last update: 31.October.2014

[Home Page]SUMER Home Page