


Next: Systems
Up: Geocentric Systems
Previous: Greenwich mean sidereal time
The geographic position of the Earth magnetic pole and the dipole moment 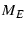 can be calculated
from the first three coefficients of the
International Geomagnetic Reference Field (IGRF)
published 5-yearly by IAGA Working Group 813. For full precision interpolate
the values
can be calculated
from the first three coefficients of the
International Geomagnetic Reference Field (IGRF)
published 5-yearly by IAGA Working Group 813. For full precision interpolate
the values
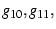 and
and 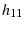 for the date requested and determine the geographic longitude
for the date requested and determine the geographic longitude
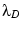 , latitude
, latitude 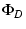 and moment
and moment 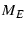 by (Hapgood, 1997; Hapgood, 1992; Kertz, 1969):
by (Hapgood, 1997; Hapgood, 1992; Kertz, 1969):
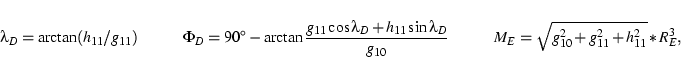 |
(21) |
where 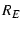 = 6378.14 km is the Earth equatorial radius and
= 6378.14 km is the Earth equatorial radius and 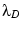 lies in the fourth quadrant.
lies in the fourth quadrant.
For the period 1975-2000 we derive following linear approximations with a precision
of  :
:
![\begin{displaymath}\lambda_D = 288^\circ.44 - 0^\circ.04236y_0 \hspace{1cm}
\Ph...
...1cm} M_E = 3.01117 - 0.00226y_0 [10^{-6} \mbox{T}\cdot R_E^3], \end{displaymath}](img147.png) |
(22) |
where 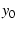 are Julian years from J2000.0.
are Julian years from J2000.0.
Markus Fraenz
2002-03-12
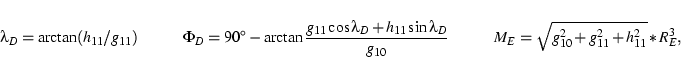
![]() :
: