 |
 |
As pointed out in the introduction transformations based on classical Keplerian elements can only achieve a limited precision. But for many applications it is useful to have approximate positions available. For this reason we describe in the following the calculation of position and velocity of objects in Keplerian orbits. There are many textbooks on this subject - we recommend Murray and Dermott (2000) but e.g. Bate et al. (1971),Danby (1988) or Heafner (1999) are also very useful. There are also some good web sites devoted to the subject19.
The gravitational motion of two bodies of mass ![]() and
and ![]() and position
vectors
and position
vectors ![]() and
and ![]() can be described in terms of the three
invariants:
gravitational parameter
can be described in terms of the three
invariants:
gravitational parameter
![]() , specific
mechanical energy
, specific
mechanical energy
![]() , and
specific angular momentum
, and
specific angular momentum
![]() , where
, where
![]() ,
,
![]() and
and
![]() .
.
![]() is the constant of gravitation whose IAU1976 value is determined by [A. K6]:
is the constant of gravitation whose IAU1976 value is determined by [A. K6]:
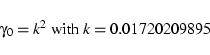 |
(24) |
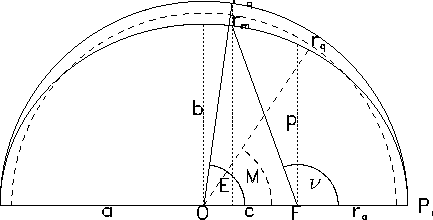
The elements of the conical orbit (shown in Fig.2) are then given as
semi-major axis
![]() and semi-minor axis
and semi-minor axis
![]() ,
or alternatively as semi-latus rectum
,
or alternatively as semi-latus rectum
![]() and
eccentricity
and
eccentricity
![]() .
Let the origin be at the focus
.
Let the origin be at the focus ![]() , the vector
, the vector ![]() then describes the motion
of the body
then describes the motion
of the body ![]() .
The true anomaly
.
The true anomaly ![]() is the angle between
is the angle between ![]() and the direction to the closest point
of the orbit (periapsis)
and can be determined from
and the direction to the closest point
of the orbit (periapsis)
and can be determined from
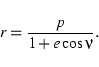 |
(25) |
Mean elements of a body in an elliptical orbit (![]() ) are defined by the motion of a point
) are defined by the motion of a point ![]() on a concentric circle with constant angular velocity
on a concentric circle with constant angular velocity
![]() and radius
and radius ![]() , such that
the orbital period
, such that
the orbital period
![]() is the same for
is the same for ![]() and
and ![]() .
The mean anomaly
.
The mean anomaly
![]() is defined as the angle between
periapsis and
is defined as the angle between
periapsis and ![]() .
Unfortunately there is no simple relation between
.
Unfortunately there is no simple relation between ![]() and the true anomaly
and the true anomaly ![]() .
To construct a relation one introduces another auxiliary concentric circle with radius
.
To construct a relation one introduces another auxiliary concentric circle with radius ![]() and defines
and defines ![]() as the point on that circle which has the same perifocal
x-coordinate as
as the point on that circle which has the same perifocal
x-coordinate as ![]() .
The eccentric anomaly
.
The eccentric anomaly ![]() is the angular distance between
is the angular distance between ![]() and the periapsis measured
from the centre and is related to the mean and true anomalies by the set of equations:
and the periapsis measured
from the centre and is related to the mean and true anomalies by the set of equations:
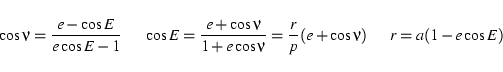 |
(27) |
Thus, if the orbital position is given as an expansion in ![]() of the
mean longitude
of the
mean longitude
![]() , the true longitude
, the true longitude
![]() can
be found by an integration of the transcendental Kepler equation.
In most cases a Newton-Raphson integration converges quickly (see Danby (1988) or Herrick (1971) for methods).
For hyperbolic orbits (
can
be found by an integration of the transcendental Kepler equation.
In most cases a Newton-Raphson integration converges quickly (see Danby (1988) or Herrick (1971) for methods).
For hyperbolic orbits (![]() ) one can as well define a mean anomaly
) one can as well define a mean anomaly
![]() but this
quantity has no direct angular interpretation. The hyperbolic eccentric anomaly
but this
quantity has no direct angular interpretation. The hyperbolic eccentric anomaly ![]() is related to
is related to ![]() and the true anomaly
and the true anomaly ![]() by
by
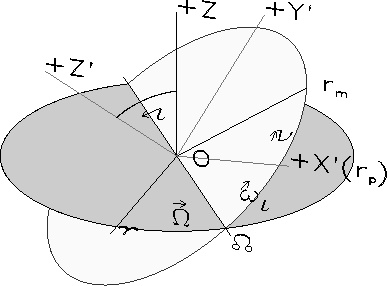 |
The orientation of an orbit with respect to a reference plane (e.g. ecliptic) with origin at the
orbital focus is defined by the inclination ![]() of the orbital plane,
the longitude of the ascending node
of the orbital plane,
the longitude of the ascending node ![]() , and the argument of
periapsis
, and the argument of
periapsis ![]() which is the angle between ascending node and periapsis
which is the angle between ascending node and periapsis ![]() (see Fig.3).
The position of the body on the orbit can then be defined by
its time of periapsis passage
(see Fig.3).
The position of the body on the orbit can then be defined by
its time of periapsis passage ![]() , its true anomaly
, its true anomaly ![]() at epoch
at epoch ![]() ,
or its true longitude
,
or its true longitude
![]() at epoch
at epoch ![]() .
The perifocal coordinate system has its X-axis from the focus to the periapsis,
and its Z-axis right-handed perpendicular to the orbital plane in the sense of orbital motion.
In this system the position and velocity vector are given by
.
The perifocal coordinate system has its X-axis from the focus to the periapsis,
and its Z-axis right-handed perpendicular to the orbital plane in the sense of orbital motion.
In this system the position and velocity vector are given by
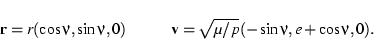 |
(29) |