Next: Planetocentric Systems
Up: Planetary Positions
Previous: Planetary Positions
Position of Earth and Moon
Tab.5 gives also ecliptic positions of Earth and Moon.
DE200 and VSOP87 give only the heliocentric position
 of the EMB. DE200 gives in addition
the geocentric position
of the EMB. DE200 gives in addition
the geocentric position
 of the Moon. If both values are given the position of the
Earth
of the Moon. If both values are given the position of the
Earth 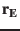 can be calculated exactly (within the IAU1976 system) using
the mass ratio Moon/Earth of
can be calculated exactly (within the IAU1976 system) using
the mass ratio Moon/Earth of
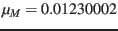 [A. K6] (or its respective value used for the ephemeris) by:
[A. K6] (or its respective value used for the ephemeris) by:
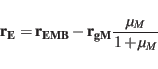 |
(31) |
The velocity vector has the same transformation. For the VSOP87 system we
apply following formula by J.L.Simon [personal communication] describing
the rotation of the Earth around the EMB:
![\begin{displaymath}\lambda_E = \lambda_{EMB} + 6''.468 \sin D \hspace{2cm} r_E = r_{EMB} + 4613 \cos D \mbox{[km]},
\end{displaymath}](img282.png) |
(32) |
where 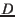 is the Delauney argument from eqn.3.5 in Simon et al. (1994):
is the Delauney argument from eqn.3.5 in Simon et al. (1994):
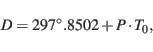 |
(33) |
where the rotation period is
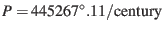 .
The Earth velocity vector
.
The Earth velocity vector 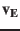 can be calculated
by
can be calculated
by
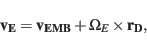 |
(34) |
where
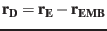 and the ecliptic angular velocity vector is given by
and the ecliptic angular velocity vector is given by
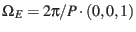 .
.
If only
 and
and 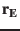 are given the ecliptic position and
velocity of the Moon can then be calculated by
are given the ecliptic position and
velocity of the Moon can then be calculated by
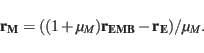 |
(35) |
But the precision of the resulting lunar velocity is rather low (190 m/s).
Neglecting the difference between
 and
and 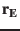 increases the total error in the Earth position to
increases the total error in the Earth position to  (Earth-EMB in Tab.5).
(Earth-EMB in Tab.5).
For slightly lower precision without solving the Kepler equation (26) the
geometric ecliptic longitude of the Earth
can be calculated by the approximation given for the Solar longitude in [A. C24]:
![\begin{displaymath}
\lambda_{geo} = \lambda_{mean} + 1^\circ.915\sin g + 0^\circ...
...{geo} = 1.00014 - 0.01671\cos g - 0.00014 \cos 2g \mbox{[AU]}, \end{displaymath}](img292.png) |
(36) |
where
 and the mean anomaly
and the mean anomaly
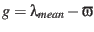 for the EMB
can be taken from Tab.4. This approximation has also been used
by Hapgood (1992). The respective precision is
for the EMB
can be taken from Tab.4. This approximation has also been used
by Hapgood (1992). The respective precision is 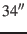 (Earth
(Earth in Tab.5).
in Tab.5).



Next: Planetocentric Systems
Up: Planetary Positions
Previous: Planetary Positions
Markus Fraenz
2017-03-13
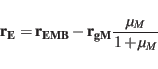
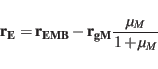
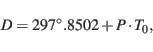
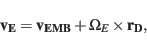
![]() and
and ![]() are given the ecliptic position and
velocity of the Moon can then be calculated by
are given the ecliptic position and
velocity of the Moon can then be calculated by