


Next: Jovian Systems
Up: Planetary Systems
Previous: Position of Earth and
Planetocentric Systems
For solar system bodies the IAU differentiates between planetocentric and
planetographic body-fixed coordinates : Planetocentric latitude
refers to the equatorial plane and the polar axis, planetographic latitude is defined
as the angle between equatorial plane and a vector through the point of interest
that is normal to the biaxial ellipsoid reference surface of the body.
Both latitudes are identical for a spherical body.
Planetocentric longitude is measured eastwards (i.e. positive in the sense of
rotation) from the prime meridian.
Planetographic longitude of the sub-observation point increases with time, i.e. to the west for
prograde rotators and to the east for retrograde rotators. All systems defined
in the following are planetocentric.
Table 6 gives the orientation of the planetary
rotation systems for all major planets at epoch 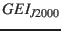 and their change with time. These are defined by the equatorial
attitude
and their change with time. These are defined by the equatorial
attitude
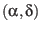 of the rotation axis and the prime meridian angle
of the rotation axis and the prime meridian angle 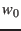 .
Data are taken from [S. Table 15.7] which is identical to the table given by Davies et al. (1996).
The ascending node right ascensions are given by
.
Data are taken from [S. Table 15.7] which is identical to the table given by Davies et al. (1996).
The ascending node right ascensions are given by
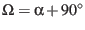 .
The respective transformation matrices are
.
The respective transformation matrices are
where 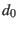 and
and 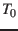 are defined in eqn.1 and 2.
are defined in eqn.1 and 2.
Table 6:
Physical Ephemeris of the Planets 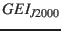 [S. Table 15.7,
A. E87]:
[S. Table 15.7,
A. E87]:
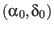 is the position of the North pole in
is the position of the North pole in 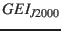 ,
,
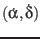 its change per Julian century
its change per Julian century 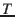 ,
,
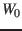 is the position of the prime meridian at
is the position of the prime meridian at 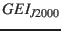 ,
,
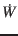 its change per day
its change per day
| Name |
![$\alpha_0 [^\circ]$](img304.png) |
![$\dot{\alpha}[^\circ/T]$](img305.png) |
![$\delta_0 [^\circ]$](img306.png) |
![$\dot{\delta}[^\circ/T]$](img307.png) |
![$W_0[^\circ] $](img308.png) |
![$\dot{W}[^\circ/d]$](img309.png) |
| Sun |
286.13 |
|
63.87 |
|
84.10 |
+14.1844000 |
| Mercury |
281.01 |
-0.003 |
61.45 |
-0.005 |
329.71 |
+6.1385025 |
| Venus |
272.72 |
|
67.15 |
|
160.26 |
-1.4813596 |
| Earth |
0.00 |
-0.641 |
90.00 |
-0.557 |
190.16 |
+360.9856235 |
| Mars |
317.681 |
-0.108 |
52.886 |
-0.061 |
176.868 |
+350.8919830 |
| Jupiter III |
268.05 |
-0.009 |
64.49 |
+0.003 |
284.95 |
+870.5360000 |
| Saturn III |
40.58 |
-0.036 |
83.54 |
-0.004 |
38.90 |
+810.7939024 |
| Uranus III |
257.43 |
|
-15.10 |
|
203.81 |
-501.1600928 |
| Neptune |
299.36 |
+0.70 |
43.46 |
-0.51 |
253.18 |
536.3128492-
0.48
 |
| (where N= |
359.28 |
+54.308) |
|
|
|
|
| Pluto |
313.02 |
|
9.09 |
|
236.77 |
-56.3623195 |
Subsections



Next: Jovian Systems
Up: Planetary Systems
Previous: Position of Earth and
Markus Fraenz
2017-03-13
![]() and their change with time. These are defined by the equatorial
attitude
and their change with time. These are defined by the equatorial
attitude
![]() of the rotation axis and the prime meridian angle
of the rotation axis and the prime meridian angle ![]() .
Data are taken from [S. Table 15.7] which is identical to the table given by Davies et al. (1996).
The ascending node right ascensions are given by
.
Data are taken from [S. Table 15.7] which is identical to the table given by Davies et al. (1996).
The ascending node right ascensions are given by
![]() .
The respective transformation matrices are
.
The respective transformation matrices are