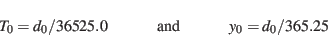Next: Precession and Nutation
Up: Heliospheric Coordinate Systems
Previous: Introduction
Table 1:
Time-scales relevant in space science [see A. B4]
| UT1 |
universal time, defined by the mean solar day |
| TAI |
international atomic time, defined by SI seconds |
| UTC |
coordinated universal time, TAI - leap seconds, broadcast standard |
| TT |
terrestrial time, TT=TAI+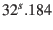 , basis for geocentric ephemeris , basis for geocentric ephemeris |
| TDB |
barycentric dynamical time, defined by the mean solar day at the |
| |
solar system barycentre, basis for solar system ephemeris |
The time-scales relevant for coordinate transformations are defined in Tab.1.
Formulae in the J2000.0 reference system are in ephemeris time  [S. 2.26, but see also Standish (1998b)], but for most purposes
of space data analysis one may neglect the
difference of less than 2 msec between
[S. 2.26, but see also Standish (1998b)], but for most purposes
of space data analysis one may neglect the
difference of less than 2 msec between  , Barycentric
Dynamical Time (TDB) and Terrestrial Time (TT) [A. B5]
and less than 0.1s between the two Universal Times (UTC, UT1)
8.
A difference between Atomic Time (TAI) and Coordinated Universal Time (UTC)
is introduced by leap-seconds tabulated in Tab.2 [A. K9 for current table]
9.
, Barycentric
Dynamical Time (TDB) and Terrestrial Time (TT) [A. B5]
and less than 0.1s between the two Universal Times (UTC, UT1)
8.
A difference between Atomic Time (TAI) and Coordinated Universal Time (UTC)
is introduced by leap-seconds tabulated in Tab.2 [A. K9 for current table]
9.
Table 2:
Leap seconds 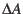 = TAI-UTC [see A. K9]
= TAI-UTC [see A. K9]
| 1972/1/1 +10s |
1972/7/1 +11s |
1973/1/1 +12s |
| 1974/1/1 +13s |
1975/1/1 +14s |
1976/1/1 +15s |
| 1977/1/1 +16s |
1978/1/1 +17s |
1979/1/1 +18s |
| 1980/1/1 +19s |
1981/7/1 +20s |
1982/7/1 +21s |
| 1983/7/1 +22s |
1985/7/1 +23s |
1988/1/1 +24s |
| 1990/1/1 +25s |
1991/1/1 +26s |
1992/7/1 +27s |
| 1993/7/1 +28s |
1994/7/1 +29s |
1996/1/1 +30s |
| 1997/7/1 +31s |
1999/1/1 +32s. |
|
Thus TDB or TT can be approximated from UTC by TDB=UTC+
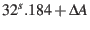 where
where 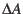 is the number of elapsed leap seconds to date. For earlier
dates Meeus (2000) gives different approximation formulae for UTC-TDB.
Spacecraft data are usually given in UTC. Relative velocities
of solar system objects are small enough (
is the number of elapsed leap seconds to date. For earlier
dates Meeus (2000) gives different approximation formulae for UTC-TDB.
Spacecraft data are usually given in UTC. Relative velocities
of solar system objects are small enough (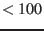 km/s) to neglect
the difference in time systems. Care must only be taken for problems
of relative timing. If high precision timing (
km/s) to neglect
the difference in time systems. Care must only be taken for problems
of relative timing. If high precision timing (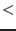 0.1s) is requested the reader
should refer to McCarthy (1996) and to the documentation of
the SPICE system (see above).
The reference points in time (epochs) for the ephemeris are given in Tab.3.
Before 1984 the ephemeris referred to B1950.0 and many spacecraft trajectory
data are still given in the older system (see Appendix).
The actual position of solar system objects and spacecraft is usually
given in an epoch of date system which means that coordinates
refer to the orientation of the Earth equator or ecliptic at the time of
measurement. We give formulae to convert from the reference epoch
to the epoch of date in the following section 2.1.
0.1s) is requested the reader
should refer to McCarthy (1996) and to the documentation of
the SPICE system (see above).
The reference points in time (epochs) for the ephemeris are given in Tab.3.
Before 1984 the ephemeris referred to B1950.0 and many spacecraft trajectory
data are still given in the older system (see Appendix).
The actual position of solar system objects and spacecraft is usually
given in an epoch of date system which means that coordinates
refer to the orientation of the Earth equator or ecliptic at the time of
measurement. We give formulae to convert from the reference epoch
to the epoch of date in the following section 2.1.
Table 3:
Epoch definitions [S. Table 15.3,
A. B4]
| J1900.0 = |
1899 December 31, 12.00TDB = |
JD 2415020.0 |
| J1950.0 = |
1950 January 1, 00.00TDB = |
JD 2433282.5 |
| J2000.0 = |
2000 January 1, 12.00TDB = |
JD 2451545.0 |
| B1950.0 = |
|
JD 2433282.42345905 |
The Julian Day Number (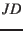 ) starts at Greenwich mean noon 4713 Jan. 1, B.C.
[S. 2.26].
The epoch day number is defined in this paper as the fractional number of days of 86400 seconds
from the epoch:
) starts at Greenwich mean noon 4713 Jan. 1, B.C.
[S. 2.26].
The epoch day number is defined in this paper as the fractional number of days of 86400 seconds
from the epoch:
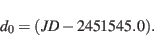 |
(1) |
Formulae from S. and A. use Julian centuries (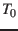 ) from J2000.0.
One Julian century has 36525 days, one Julian year has 365.25 days, s.t. [S. T3.222.2]
) from J2000.0.
One Julian century has 36525 days, one Julian year has 365.25 days, s.t. [S. T3.222.2]
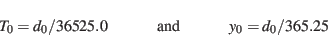 |
(2) |
We use this notation throughout the paper. When the astronomical reference
systems eventually switch to the next epoch (presumably J2050.0) formulae
given in this paper have to be adapted.
Subsections



Next: Precession and Nutation
Up: Heliospheric Coordinate Systems
Previous: Introduction
Markus Fraenz
2017-03-13