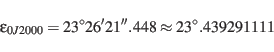 |
(3) |
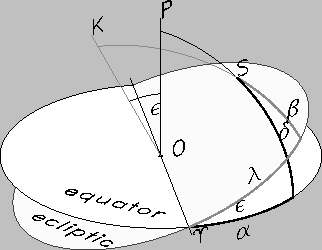
The intersection of the Earth equatorial plane and the Earth orbital plane (ecliptic)
defines the line of the equinoxes (Fig.1). The ascending node
of the geocentric ecliptic defines the vernal equinox (first point of Aries).
The obliquity of the ecliptic at epoch J2000.0 with respect to the mean
equator at epoch J2000.0 is given by [A. K6]
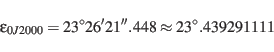 |
(3) |
The orientation of both planes changes over time by solar, lunar and planetary gravitational forces on the Earth axis and orbit. The continuous change is called 'general precession', the periodic change 'nutation'. Mean quantities include precessional corrections, true quantities both precessional and nutational corrections.
The mean obliquity of the ecliptic of date with respect to the mean
equator of date is given by [S. 3.222-1,A. B18]
| (4) | |||
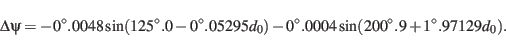 |
(6) |
To achieve higher precision one has to add further terms for the series expansion for nutation from [S. Tables .3.222.1-3.224.2]10.
The orientation of the ecliptic plane of date (![]() ) with respect to the
the ecliptic plane at another date (
) with respect to the
the ecliptic plane at another date (![]() ) is defined by the inclination
) is defined by the inclination ![]() ,
the ascending node longitude
,
the ascending node longitude ![]() of the plane of date
of the plane of date ![]() relative to the plane of date
relative to the plane of date ![]() ,
and the difference in the angular distances
,
and the difference in the angular distances ![]() of the vernal equinoxes from the ascending node.
Values for J2000.0 are given in [S. Table 3.211.1]:
of the vernal equinoxes from the ascending node.
Values for J2000.0 are given in [S. Table 3.211.1]:
| (8) | |||
Coordinates defined on the equator of epoch are transformed to the
equator of date by the Eulerian precession matrix
| (11) | |||
Hapgood (1997) gives only the first order transformation between
epoch of J2000.0 and epoch of date which is a reduction of the above
formulae and also given to higher precision in [A. B18]:
| (12) | |||
For the heliocentric position of the Earth a complete neglect of
precession results in an error of ![]() for the period
1950-2050, a neglect of nutation results in an error of
for the period
1950-2050, a neglect of nutation results in an error of
![]() .
Using first order nutation and precession reduces the error to
.
Using first order nutation and precession reduces the error to
![]() .
.
 |