


Next: Velocity Transformations
Up: Appendix
Previous: Appendix
Figure:
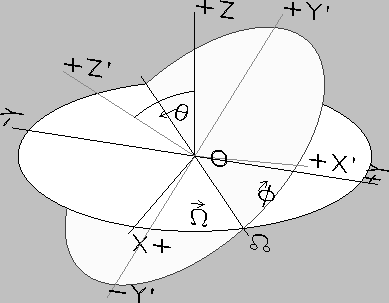
Eulerian Rotation
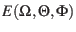 (after Madelung (1964)): the transformation between system
(after Madelung (1964)): the transformation between system 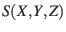 and
system
and
system 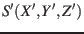 can be expressed by the three right-handed principal rotations:
1.
can be expressed by the three right-handed principal rotations:
1. 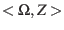 around the
around the 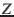 -axis towards the ascending node
-axis towards the ascending node 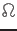 , 2.
, 2.
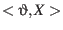 around the
ascending node axis, 3.
around the
ascending node axis, 3. 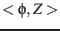 around the
around the 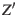 -axis towards the
-axis towards the 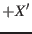 -axis.
-axis.
 |
In this paper we describe transformations between
cartesian coordinate systems in Euclidean space.
Let system S be defined by the orthonormal right-handed basis vectors 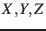 and
system
and
system 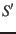 by the orthonormal right-handed basis vectors
by the orthonormal right-handed basis vectors 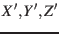 with a common origin
with a common origin 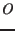 .
The position of system
.
The position of system 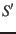 in system
in system 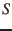 is then defined by the angular
coordinates of its pole (
is then defined by the angular
coordinates of its pole (
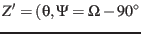 )) and the
prime meridian angle
)) and the
prime meridian angle 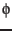 (see Fig.4) which is
the angular distance between prime meridian
(see Fig.4) which is
the angular distance between prime meridian 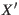 and ascending node
and ascending node 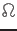 .
The Eulerian
transformation matrix from
.
The Eulerian
transformation matrix from 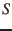 to
to 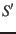 is then defined by (Madelung, 1964):
is then defined by (Madelung, 1964):
| |
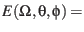 |
 |
(39) |
Such that a vector 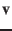 given in
given in 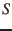 has coordinates
has coordinates
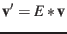 in
in 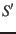 .
This corresponds to three principal rotations:
.
This corresponds to three principal rotations:
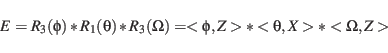 |
(40) |
in the notation of Hapgood (1992) where '*' denotes matrix multiplication.
The three principal rotations
are on the other hand given by
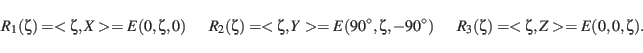 |
(41) |
Note that all rotation matrices are orthogonal, s.t.  and transformations
between all systems defined in this paper can easily be calculated
by a series of matrix multiplications.
and transformations
between all systems defined in this paper can easily be calculated
by a series of matrix multiplications.



Next: Velocity Transformations
Up: Appendix
Previous: Appendix
Markus Fraenz
2017-03-13


![]() and
system
and
system ![]() by the orthonormal right-handed basis vectors
by the orthonormal right-handed basis vectors ![]() with a common origin
with a common origin ![]() .
The position of system
.
The position of system ![]() in system
in system ![]() is then defined by the angular
coordinates of its pole (
is then defined by the angular
coordinates of its pole (
![]() )) and the
prime meridian angle
)) and the
prime meridian angle ![]() (see Fig.4) which is
the angular distance between prime meridian
(see Fig.4) which is
the angular distance between prime meridian ![]() and ascending node
and ascending node ![]() .
The Eulerian
transformation matrix from
.
The Eulerian
transformation matrix from ![]() to
to ![]() is then defined by (Madelung, 1964):
is then defined by (Madelung, 1964):

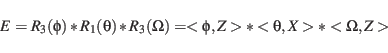
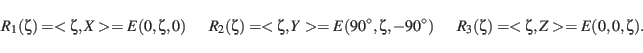
![]() and transformations
between all systems defined in this paper can easily be calculated
by a series of matrix multiplications.
and transformations
between all systems defined in this paper can easily be calculated
by a series of matrix multiplications.