


Next: Light Aberration
Up: Appendix
Previous: Eulerian Rotation
While position and magnetic field vectors are independent of the relative motion
of the coordinate system this is not true for other vectors for example for
the solar wind velocity vector. Usually this vector is originally given
in a spacecraft reference frame. For solar wind studies it is
advisable to subtract the effect of the spacecraft motion
relative to a heliocentric inertial system. If the spacecraft
velocity vector is not provided together with the positional data
the velocity can be calculated from the temporal derivative of
the position time series. The velocity vector in the transformed system is generally given by
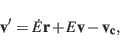 |
(42) |
where 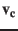 is the relative speed of the system origins and
is the relative speed of the system origins and
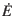 is the temporal derivative of the rotation matrix:
is the temporal derivative of the rotation matrix:
For the transformation into planetocentric systems 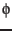 is the only angle changing rapidly such that
is the only angle changing rapidly such that
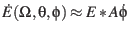 .
.
One of the most common transformations is the transformation from a heliocentric inertial
system like  to a geocentric rotating system like
to a geocentric rotating system like 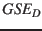 . Since
. Since
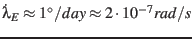 the rotational part of the velocity transformation can be neglected
for geocentric distances of less than
the rotational part of the velocity transformation can be neglected
for geocentric distances of less than 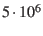 km to keep an accuracy of
km to keep an accuracy of 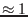 km/s.
In that case the transformation reduces to the subtraction of the orbital
velocity of the Earth which in the ecliptic system is given by
km/s.
In that case the transformation reduces to the subtraction of the orbital
velocity of the Earth which in the ecliptic system is given by
 |
(44) |
where 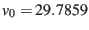 km/s is the mean orbital velocity of the Earth and
km/s is the mean orbital velocity of the Earth and 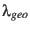 the Earth longitude
defined in eqn.36.
the Earth longitude
defined in eqn.36.



Next: Light Aberration
Up: Appendix
Previous: Eulerian Rotation
Markus Fraenz
2017-03-13
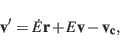
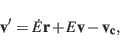
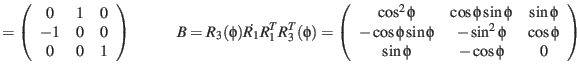
![]() to a geocentric rotating system like
to a geocentric rotating system like ![]() . Since
. Since
![]() the rotational part of the velocity transformation can be neglected
for geocentric distances of less than
the rotational part of the velocity transformation can be neglected
for geocentric distances of less than ![]() km to keep an accuracy of
km to keep an accuracy of ![]() km/s.
In that case the transformation reduces to the subtraction of the orbital
velocity of the Earth which in the ecliptic system is given by
km/s.
In that case the transformation reduces to the subtraction of the orbital
velocity of the Earth which in the ecliptic system is given by
