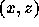We use the equations of ideal stationary magnetohydrodynamics, which are a subgroup
of the MHD-equations (1 - 8), to calculate
stationary state helmet streamer configurations.
The equations of stationary ideal MHD are given by
equations (1 - 6), where the right-hand side of equations (1-3)
is identical zero.
With the help of our basic assumptions we simplify the equations of stationary ideal MHD.
We illustrate our method in Cartesian geometry without gravitation, magnetic shear and
plasma flow. In a two-dimensional Cartesian geometry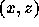 
we represent the magnetic field as
and find from equation (1) that the flux function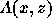 
has to obey the equation
Unfortunately it is not possible to derive the function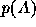 
from the observations. We use the
popular choice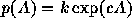 
. To calculate triple streamers, the separatrices
between the middle and outer streamers have to be calculated self-consistently with
the solution. We label the separatrix field line with a value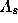 
of the flux
function and use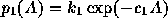 
for the middle streamer and
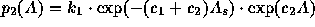for the outer streamers (
).
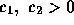This choice ensures, that both pressure
function coincide on the separatrices.
If we assume that the magnetic field
perpendicular to the photosphere (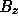
in the Cartesian geometry) is much larger than the parallel component (
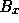in the Cartesian geometry),
we can use the
method of asymptotic expansion [Schindler1972] and apply it to Eq. (10).
Mathematically stretched configurations are characterized by
the ordering
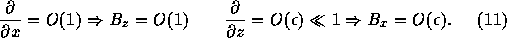
If we neglect terms of the order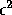 
in Eq. (10)
we obtain after one integration with respect to x and after solving
this differential equation by separation [Birn et al.1975]
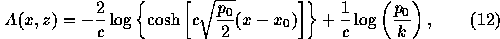
where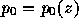 
is an integration constant (total pressure on the z-axis), which depends parametrically on z. One can choose 
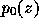arbitrarily to fit the model to the
observations. To derive triple streamers, we use 
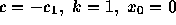in the middle
streamer and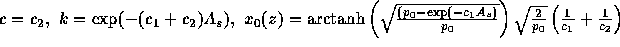 
in the right outer streamer, while the left outer streamer is calculated by a symmetry assumption. Note that 
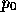and thus
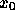depends parametrically on z. The separatrix field line
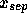, which separates the middle streamer and the right outer streamer is given analytically by
.
Thus we derive selfconsistent, analytical helmet streamer configurations with triple structures. The method works similar in spherical geometry and one can include the solar gravitation, magnetic shear and stationary plasma flow [Wiegelmann et al.1998].
