 | 
|
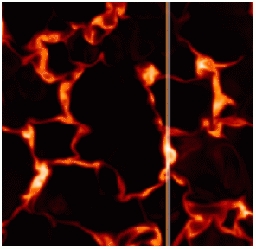
Fig 1: Image of modulus of the Stokes V parameter integrated over wavelength for the infrared line FeI (15648.5A) as a diagnostic for vertical magnetic field.
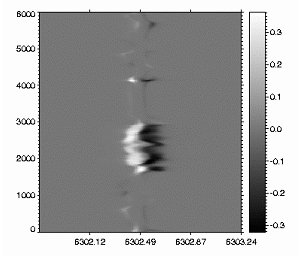
| Fig 2: Spectrum of Stokes V (circular polarization).
The V parameter shows a pronounced signal in the strong flux
concentration and a weaker signal where the "slit" traverses a narrow
intergranular magnetic flux sheet.
|
In order to compare the results of magnetohydrodynamical simulations of photospheric magneto-convection with observations, spectral diagnostics is required.
We carry out spectral diagnostics of 3-dimensional MHD simulations. The simulations, which include radiative transfer and partial ionization, use a computational box of 6000 x 6000 x 1400 km3 size and an initial vertical magnetic field of 200 G (see Fig 1).
The spectral diagnostics is carried out with the STOPRO code (written by S.K. Solanki and C. Frutiger), which calculates Stokes profiles (see, for example, Fig 2) on the basis of the atomic data and the atmospheric parameters like temperature, pressure, magnetic field, and velocity.
References
Back to top
Stability of a magnetic flux tube in helical flow
F. Kolesnikov, M Schüssler, D, Schmitt
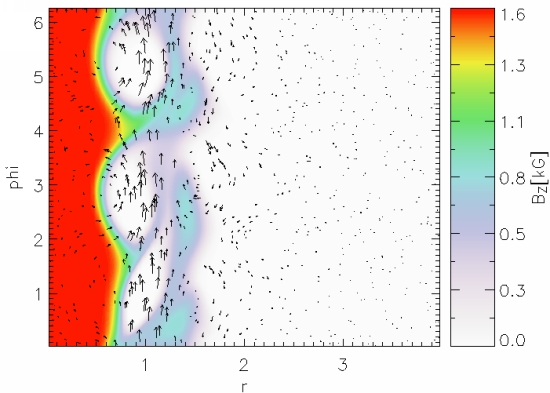
Figure 1: An unstable flow configuration. The radial component of the velocity was perturbed in the transition
layer. The vertical component of the magnetic field is shown in color, arrows represent the perturbation velocity field (initial velocity field is subtracted). The
eigen mode with the azimuthal wavenumber m=3 is growing.
Onset of the Kelvin-Helmholtz instability of an axisymmetric flux tube in a vortex flow.
Magnetic flux concentrations in the solar (sub)photosphere are surrounded by strong downflows, which come into swirling motion owing to the conservation of angular momentum. While such a whirl flow can stabilize a magnetic flux tube against the MHD fluting instability, it potentially becomes subject to the Kelvin-Helmholtz and shear instabilities near the edge of the flux tube, which may lead to twisting of the magnetic field and perhaps even to the disruption of the magnetic structure. As a first step towards studying the relevance of such instabilities, we investigate the stability of an incompressible flow with longitudinal and azimuthal (whirl) components surrounding a cylinder with a uniform longitudinal magnetic field. We find that a sharp jump of the azimuthal flow component at the cylinder boundary always leads to a Kelvin-Helmholtz-type instability for sufficiently small wavelengths of the perturbation. On the other hand, a smooth and wide enough transition of the azimuthal velocity towards the surface of the cylinder leads to stable configurations, even for a discontinuous profile of the longitudinal flow.
Magnetic flux concentrations in the solar (sub)photosphere are surrounded by strong downflows, which come into swirling motion owing to the conservation of angular momentum. While such a whirl flow can stabilize a magnetic flux tube against the MHD fluting instability, it potentially becomes subject to the Kelvin-Helmholtz and shear instabilities near the edge of the flux tube, which may lead to twisting of the magnetic field and perhaps even to the disruption of the magnetic structure. As a first step towards studying the relevance of such instabilities, we investigate the stability of an incompressible flow with longitudinal and azimuthal (whirl) components surrounding a cylinder with a uniform longitudinal magnetic field. We find that a sharp jump of the azimuthal flow component at the cylinder boundary always leads to a Kelvin-Helmholtz-type instability for sufficiently small wavelengths of the perturbation. On the other hand, a smooth and wide enough transition of the azimuthal velocity towards the surface of the cylinder leads to stable configurations, even for a discontinuous profile of the longitudinal flow.
Reference
Back to top
Dynamics of Magnetic Flux Configurations in the deep Convection Zone
M. Rempel (HAO, Boulder), M Schüssler
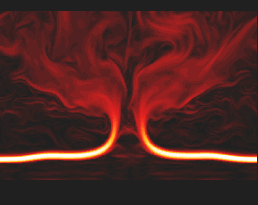
Color-coded magnetic field strength of a flux sheet after it has exploded due to a
buoyancy-driven instability. The horizontal part of the sheet is partly evacuated,
leading to a significant increase in field strength. With this mechanism, field-amplification
at the base of the convection zone up to 10 Tesla becomes possible within a few months.
References
Back to top
Magnetic field reversals and secular variation in a bistable geodynamo model
D. Schmitt, P. Hoyng (Utrecht), M. Ossendrijver (Freiburg)
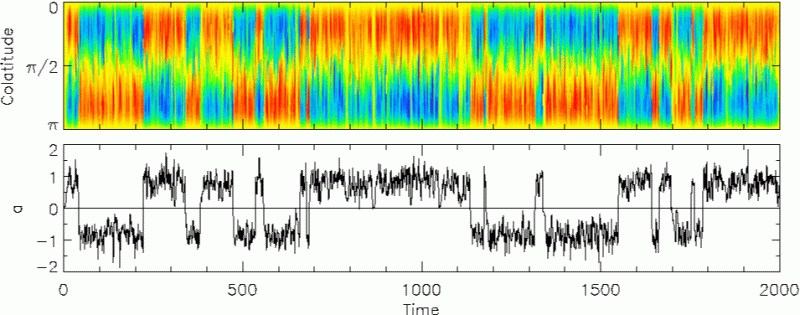
Helicity fluctuations in a mean-field dynamo model lead to a secular variation
of the dipole moment and occasionally to sudden polarity reversals. The
fluctuations perturb the fundamental dynamo mode, a non-oscillatory dipole,
and excite higher modes. This results in stochastic oscillations of the
dipole field amplitude in a bistable potential with minima representing
normal and reversed polarity, and occasional jumps between them. A relation
between the intensity variation and the reversal rate is found, and the
observed amplitude distribution of the dipole field is reproduced.
The figure displays the toroidal magnetic field as a function of colatitude
and time (in units of the diffusion time) with red and blue indicating the
two polarities. In the lower panel the dipole amplitude is plotted versus
time.
References
Back to top
Mean-field coefficients for geodynamo models
M. Schrinner, K.-H. Rädler (Potsdam), D. Schmitt, M. Rheinhardt (Potsdam), U. Christensen
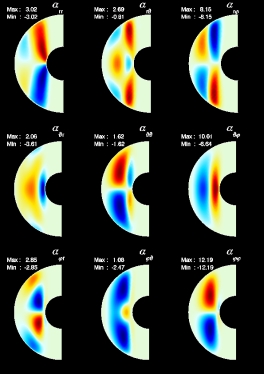

Large scale magnetic fields in the Earth and other planets, in the
Sun and other active stars and also in spiral galaxies are apparently
maintained by hydromagnetic dynamos. Concerning the geodynamo there
are now dynamo models available that reproduce many features of the
Earth's magnetic field very successfully without making any use of
mean-field theory. One aim of our work is to compare these results
with those based on mean-field theory. This will give an estimation
on the reliability and validity of mean-field theory which still is
used in dynamo models for various astronomical objects. Within
mean-field models the mean-field coefficients a and
b are decisive quantities in order to describe dynamo
action. We use a dynamically computed velocity field with the
aim to calculate mean-field coefficients for the earth's outer core.
The 9 components of an a-tensor are shown in the figure on the left. In the
other figure, a comparison between direct numerical simualtions and
mean-field calculations is presented. While a mean-field model which
relies on the full set of determined mean-field coefficients (right, second row)
reproduces the azimuthally averaged field given by a direct
numerical simulation (right, first row) in great detail, an isotropic
approximation for a and b (right, last row) leads to
deviations in the amplitudes of the poloidal field and to a different
field topology of the induced toroidal field.
Mean-field concept and direct numerical simulations of rotating magnetoconvection and the geodynamo, M. Schrinner, Rädler, K.-H., Schmitt, D., Rheinhardt, M., Christensen, U.; Geophys. Astrophys. Fluid Dyn., 101, 81 (2007)
Mean-field view on rotating magnetoconvection and a geodynamo model, M. Schrinner, K.-H. Raedler, D. Schmitt, M. Rheinhardt, U. Christensen, Astron. Nachr./ AN 326, No. 3/4, 245-249 , 2005.
References
Back to top
Saturation properties of the Archontis dynamo
R. Cameron, D. Galloway (Univ. of Sydney)
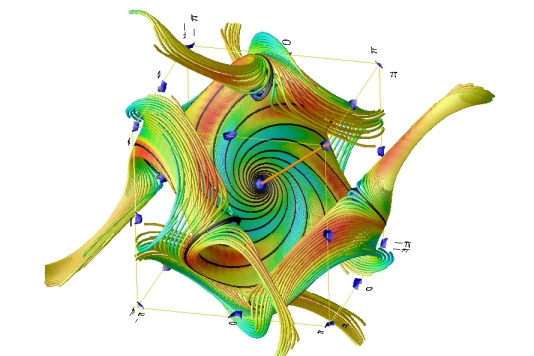
This image shows the one-dimensional (orange line) and two-dimensional (color-coded surface) manifolds, as well as heteroclinic orbits (black lines and the one-dimensional manifold) associated with a stagnation point of the Archontis dynamo. The Archontis dynamo is the first known example of a dynamo which, at low resistivity and viscosity, is "Alfvenic" when it saturates (ie the flow everywhere is at the local Alfven speed). Its properties, including the stagnation points, stable and unstable manifolds, and heteroclinic orbits are currently being studied.
Reference
Back to top
Flux tube dynamics in binaries and giant stars
V. Holzwarth, M. Schüssler

An erupting flux tube in a model with 1 solar mass at an age of 12.14 Gyr. Subsequent
flux tube-configurations are shown until the rising loop has nearly reached the
stellar surface. For models with a smaller ratio of core radius to stellar radius
the flux tube becomes trapped as the inward directed magnetic tension increases due
to geometrical effects. This could explain the decline in X-ray emission of cool
giant stars since flux tube-trapping terminates solar-like activity with large bipolar
magnetic regions and extended coronal loops.
References
Back to top
Spatial equilibrium distribution of plasma in rotating dipolar fields
O. Preuss, V. Holzwarth, S.K. Solanki, M Schüssler
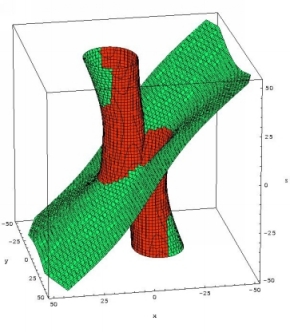
The search for stable equilibrium distributions of plasma which is
trapped in a rotating dipolar field is of interest for many
applications in stellar astrophysics, mainly for the problem of
magnetically confined circumstellar matter around hot stars. Based on
the balance between gravitational and centrifugal forces for a
charged particle on a magnetic field line, the picture shows a
3-dimensional visualization of stable (green) and unstable (red)
equilibrium positions for an oblique dipolar rotator (i.e., a star
with rotation and magnetic dipole axis inclined relative to each other).
For the special case of aligned dipole and rotation axes we a
stable equatorial disc in agreement with observations of Be stars.
If the axes are not aligned, as in the picture, the disc is warped and
additional regions of stable equilibrium positions appear.
Reference
Back to top
Last modified: Mon Sep 17 18:06:42 CEST 2007