Note that in the version of this paper published in Planetary&Space Science, 50, 217ff, the date taken for this example is erroneously given as Aug 28, 1996 16:46:00 UTC, not TT.
We assume that a spacecraft position is given in true geographic
coordinates (![]() ) on the date Aug 28, 1996 16:46:00 TT
(JD 2450324.19861111). Numerical results are given in Tab.8
(We have chosen this date and position because software by M. Hapgood [personal
communication] uses these values as a reference set.)
The Julian century for this date is
) on the date Aug 28, 1996 16:46:00 TT
(JD 2450324.19861111). Numerical results are given in Tab.8
(We have chosen this date and position because software by M. Hapgood [personal
communication] uses these values as a reference set.)
The Julian century for this date is
![]() (eqn.2).
In the following we apply the formulas of section 3.3.3.
To convert from
(eqn.2).
In the following we apply the formulas of section 3.3.3.
To convert from ![]() to
to ![]() we calculate
we calculate
![]() by eqn.20. To convert from the true equator of date to the mean
equator of date we have to apply the nutation matrix (eqn.7)
with
by eqn.20. To convert from the true equator of date to the mean
equator of date we have to apply the nutation matrix (eqn.7)
with
![]() .
Then we apply
.
Then we apply
![]() to
transform to the mean ecliptic of date (
to
transform to the mean ecliptic of date (![]() ), the precession matrix (eqn.9)
to transform to the ecliptic of J2000 (
), the precession matrix (eqn.9)
to transform to the ecliptic of J2000 (![]() ) and
) and
![]() to transform to the equator of J2000 (
to transform to the equator of J2000 (![]() ).
(The vector is still geocentric since we did not apply a translation. So it might
better be called
).
(The vector is still geocentric since we did not apply a translation. So it might
better be called ![]() etc. but we stick with the
etc. but we stick with the ![]() to avoid more acronyms.)
to avoid more acronyms.)
We use
![]() and
and ![]() of section 3.2.2
to transform to the heliographic systems. To transform to geocentric Earth Ecliptic (
of section 3.2.2
to transform to the heliographic systems. To transform to geocentric Earth Ecliptic (![]() ) coordinates
we use
) coordinates
we use
![]() from section 3.2.2,
for
from section 3.2.2,
for ![]() we use
we use
![]() (eqn.17).
To transform to
(eqn.17).
To transform to ![]() with low precision we use the ecliptic longitude of the Earth
with low precision we use the ecliptic longitude of the Earth
![]() (eqn.36).
To transform to
(eqn.36).
To transform to ![]() we use the Earth dipole position
we use the Earth dipole position
![]() (eqn.22)
and angles
(eqn.22)
and angles
![]() .
.
To proceed to position dependent systems we now determine the Earth position to a higher
precision using the orbital elements of the EMB from Tab.4 corrected by
Tab.6 of Simon et al. (1994) (values available on our website):
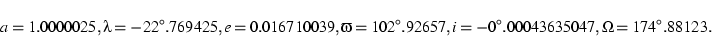 |
(45) |
![\begin{displaymath}\lambda_{EMB}= -24^\circ.305587, \beta_{EMB} = -0^\circ.00014340633, r_{EMB} = 1.0099340\mbox{[AU]}. \end{displaymath}](img407.png) |
(46) |
![\begin{displaymath}\lambda_{E}= -24^\circ.305442, r_{E} = 1.0099033\mbox{[AU]}. \end{displaymath}](img409.png) |
(47) |
![\begin{displaymath}X_E = 21579.585 [R_E], Y_E = -9767.205[R_E], Z_E = 0.000016[R_E] \end{displaymath}](img410.png) |
(48) |
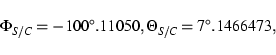 |
(49) |