Realistic Simulation of Solar Magnetic Structure

Home

People

Code

Results

Publications

MHD Group

Solar MHD at the Max Planck Institute for Solar System Research  

Results

Penumbral structure

Turbulent magnetic fields

Magneto-convection in a sunspot umbra

A Solar surface dynamo

Current sheets in the upper photosphere

Magneto-convection in the solar photosphere

Decay of bipolar fields

Simulation of solar pores

Magnetic flux emergence

Non-grey radiative transfer in radiative MHD simulations
 

Penumbral Structure

(M. Rempel, M. Schüssler, R. Cameron, M. Knölker )


Figure 1: Inclination angle of magnetic field in and around a (simulated) sunspot (black is vertical field, white is horizontal).
The structure of sunspots, including their umbra, penumbra and the surrounding quiet-Sun has been simulated. The simulations reveal the convective nature of the penumbra. The presence of the inclined magnetic fields in the penumbra causes the convective motions to be highly anistopic, in terms of intensity (penumbral filaments with dark-cores, outflows of up to 10km/s (the Evershed flow), and magnetic fields.

References

  • Penumbral Structure and Outflows in Simulated Sunspot , Rempel, M., Schüssler, M., Cameron, R., Knölker, M., Science, Volume 325, 171-174 (2009).
  • Radiative Magnetohydrodynamic Simulation of Sunspot Structure , Rempel, M., Schüssler, M., Knölker, M., ApJ, Volume 691, 640-649 (2009).

    -> back to top

    		•

    Turbulent magnetic fields

    (J. Pietarila Graham, S. Danilovic, M. Schüssler )

    Observations of small-scale magnetic fields fields from Hinode and numerical simulations of dynamo action in the photospheric layers of the Sun are compared. Using turbulence theory to motivate self-similar scaling laws, a lower bound of 50G is derived for the unsigned quiet-Sun vertical flux. This agrees with our MURaM simulation-based estimate and (considering vector magnitudes) resolves the discrepancy between Hanle and Zeeman observations.

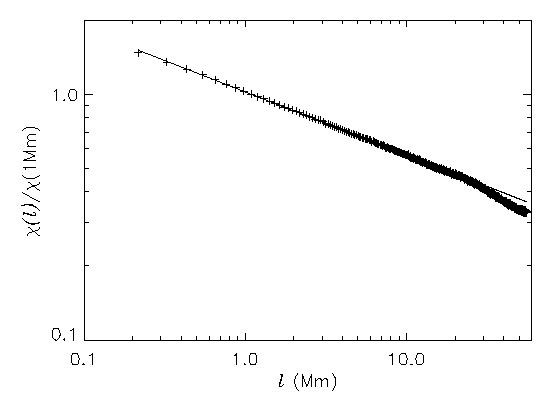
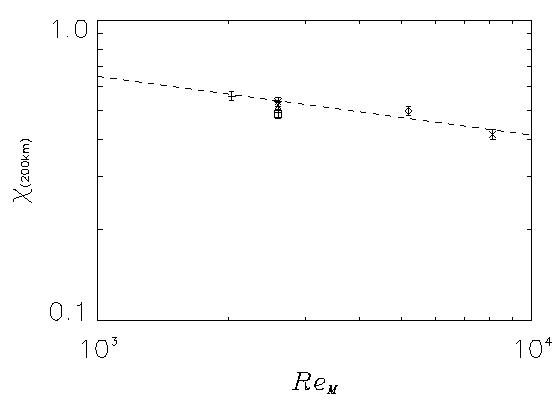
    Figure 1. Left: Portion of magnetic flux remaining after averaging over boxes of increasing size (from Hinode observation). A self-similar power-law is abundantly clear for 2 decades of length scales down to the resolution limit. Right: Flux remaining after averaging over 200 km X 200 km boxes for MURaM as a function of magnetic Reynolds number, ReM. Extrapolation to solar ReM indicates at least 80% cancellation at 200 km resolution.

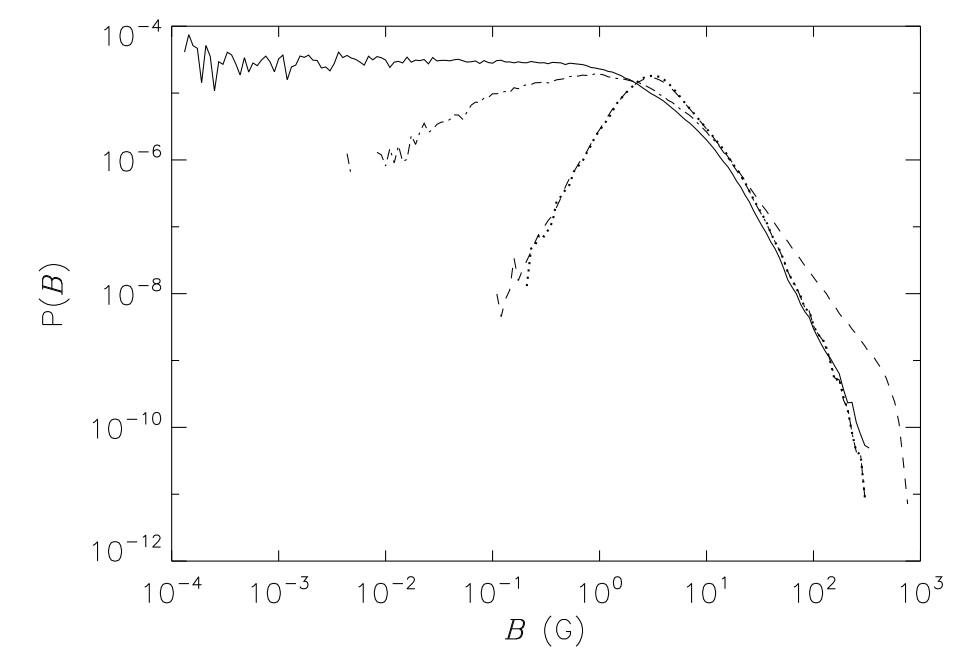
    Figure 2. Probability distribution functions of magnetic field strengths from the simulations (solid line), from the Hinode observations (dashed lines), the inversions of synthetic stokes-diagnostics created from the simulations (dash dot) and when an observational noise level of 0.0011 is added (dotted line). The observational peak that was previously considered solar is seen to be solely due to noise.

    References

  • Turbulent Magnetic Fields in the Quiet Sun: Implications of Hinode Observations and Small-Scale Dynamo Simulations, Pietarila Graham, J., Danilovic, S., Schüssler, M., ApJ, Volume 693, 1728-1735 (2009).

    -> back to top

    		•

    Identification of MURaM dynamo as a turbulent small-scale dynamo

    (J. Pietarila Graham, R. Cameron, M. Schüssler )

    Spectral transfer analysis of the MURaM dynamo rules out the tangling of magnetic field lines (turbulent cascade) and Alfvénization of turbulent velocity fluctuations ("turbulent induction") as sources of small-scale magnetic field (see Figure 1). Rather, small-scale fluid motions stretch small-scale magnetic field to produce more small-scale magnetic field and the scales involved become smaller with increasing Reynolds number. This is a small-scale turbulent dynamo.

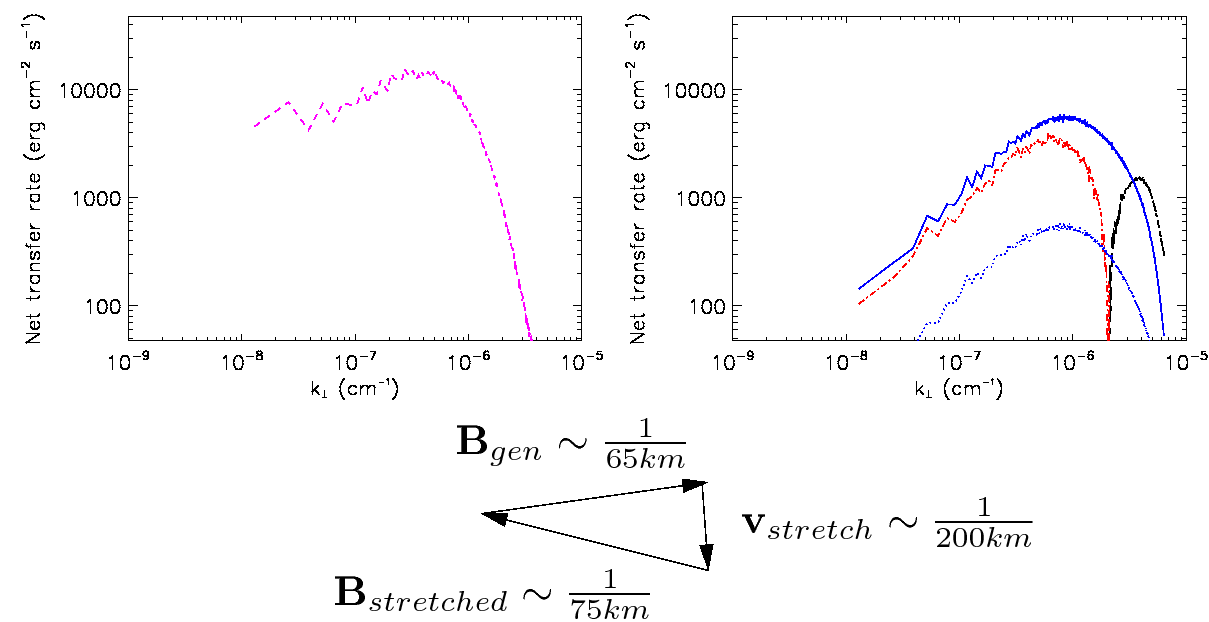
    Figure 1. Transfer analysis of MURaM surface dynamo. Left: Work against Lorentz force versus horizontal spatial frequency shows that fluid motions at scales near 200 km stretch magnetic field lines (dynamo). Right: Rate of magnetic energy production by stretching (blue solid) and compression (blue dotted), magnetic energy lost (red) and gained (black) from the turbulent cascade versus horizontal spatial frequency. Magnetic field is produced predominantly at scales near 65 km from stretching motions. Bottom: Triadic transfer indicates the magnetic field that is stretched has scales near 75 km. All scales are well below the 1000 km granulation scale, identifying the dynamo mechanism as a turbulent small-scale dynamo.

    Figure 2. Vertical cuts of Top: Real-space analog of blue solid line from Figure 1: rate of magnetic energy production by stretching and Bottom: vertical velocity (dark for down-flows). Down-flow plumes are the site of dynamo generation.

    -> back to top

    Magnetoconvection in a sunspot umbra

    ( M. Schüssler, A. Vögler)


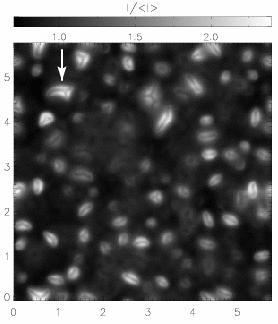
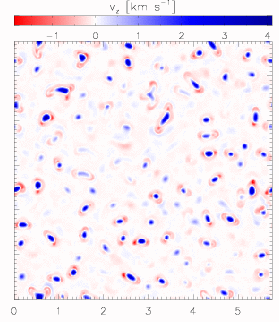
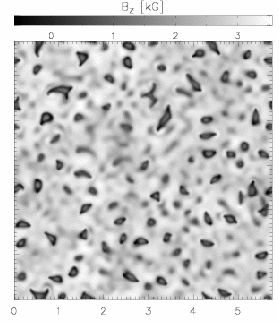
    Figure 1: Left frame: brightness; Middle: vertical velocity (blue: upflows, red: downflows, white: stagnant Right column: vertical magnetic field at <τ> = 1.
    The strong magnetic field (from 2000 G to more than 4000 G) in a sunspot umbra suppresses the normal granular convection. Simulations with the MURaM code have shown that the convective energy transport instead occurs in the form of narrow hot upflow plumes, which appear as bright patches before a dark background (see brightness image to the left, spatial scale in Mm). Their sizes, contrasts and lifetimes are similar to the observed properties of so-called `umbral dots'. The vertical velocity image (middle panel) taken near the level of optical depth unity shows that the upflows in the plumes (blue) are surrounded by narrow downflow channels (red). The strong expansion of the upflow plumes with height due to the pressure stratification leads to a strong expansion of the plumes and a concomitant reduction of the magnetic field strength (right panel) in the upper layers. Near optical depth unity, the hot material in the plume loses its buoyancy and piles up in a cusp-shaped structure, leading to the appearance of dark lanes in the brightness image.

    Reference

  • Magnetoconvection in a Sunspot Umbra, Schüssler, M. & Vögler, V., ApJ, Volume 641, Issue 1, pp. L73-L76 (2006).

    -> back to top

    		•

    A solar surface dynamo

    ( A. Vögler, M. Schüssler)


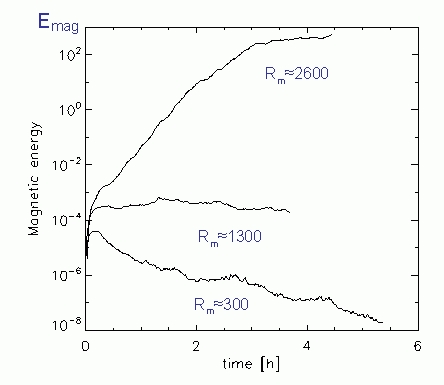
    Figure 1: Left frame: brightness; Middle: vertical velocity (blue: upflows, red: downflows, white: stagnant Right column: vertical magnetic field at <τ> = 1.
    Various observations indicate the existence of significant amounts of magnetic flux ubiquitous in the `quiet Sun', i.e., outside active regions, with mixed polarity on small scales. Since idealized Boussinesq closed-box simulations of Cattaneo (ApJ, 1999) showed dynamo action of non-helical instationary convection, the existence of a similar process based upon granular convection of the Sun has been discussed. Removing the idealizations in a realistic simulation with the MURaM code, we have found that solar surface convection seems indeed capable of supporting a dynamo process: for sufficiently large magnetic Reynolds number, the magnetic energy of an initial weak seed field grows exponentially and saturates at levels consistent with the observational inferences. The generated surface field has a small/scale structure with mixed polarity (right panel: vertical field image near optical unity; the size of the magnified inset is about 1200 km x 1200 km on the Sun) and shows an association with the intergranular downflow lanes.

    Reference

  • A solar surface dynamo, Vögler, A.; Schüssler, M., Astron. Astrophys., 465, L43-L46 (2007).

    -> back to top

    		•

    Current sheets in the upper photosphere

    ( M. Schüssler, R.Cameron, A. Vögler)


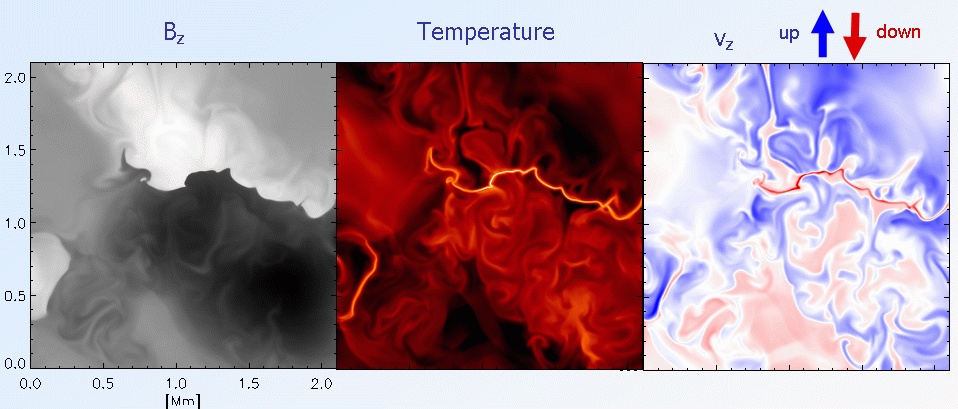
    Figure 1: Left: vertical magnetic field at 600km above <τ> = 1 middle: Temperature; Right: vertical velocity (blue: upflows, red: downflows, white: stagnant.
    Simulations of mixed-polarity magnetic fields with the MURaM code reveal the appearance of current sheets between field patches of opposite polarity in the upper photosphere. The image shows a small section from the highest-resolution and biggest simulation of solar magneto-convection carried out so far: 5 km horizontal numerical cell size and 1152 x 1152 x 200 cells. The image shows horizontal cuts of a small part of the computational box at about 600 km above optical depth unity (visible surface). The vertical magnetic field (left, black/white color scale for the two polarities) shows a sharp polarity inversion, which is outlined by a hot region in the temperature image (middle) and associated with a strong downflow exceeding 10 km/s in the vertical velocity image (right). The structure displays all characteristic features of a `textbook' current sheet with reconnection: a quasi-discontinuity of the magnetic field, local Joule heating and temperature peak (exceeding 9000 K), horizontal inflow and vertical outflow, local maxima of gas pressure and density. Possible observational signatures are currently evaluated.

    -> back to top

    Magneto-convection in the solar photosphere: From Quiet Sun to strong plage

    (A. Vögler, M. Schüssler)

    Using MURaM, we carried out a series of simulation runs to study the dependence of photospheric magneto-convection on the amount of magnetic flux. In each of the runs an initially vertical, homogeneous magnetic field of strength B0 was introduced into fully developed hydrodynamic convection. We considered five cases with B0 = 10 G, 50 G, 200 G, 400 G, and 800 G. Fig. 1 shows snapshots of brightness, magnetic field strength at<τ> = 1, and vertical verlocity at<τ> = 1.


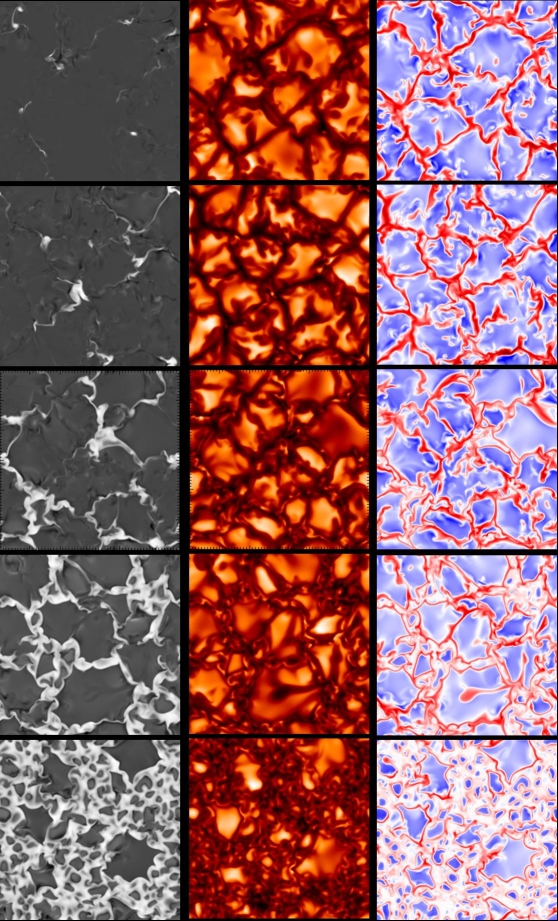
    Figure 1: Snapshots for the cases with an initial field strength of 10 G, 50 G, 200 G, 400 G, and 800 G (from top to bottom). Left column: vertical magnetic field at <τ> = 1; Middle column: brightness; Right column: vertical velocity (blue: upflows, red: downflows, white: stagnant).
    As a result of flux expulsion and convective field amplification, most of the magnetic flux forms partially evacuated kilogauss flux concentrations embedded in the network of intergranular downflows. In the case B0=10 G these field concentrations are isolated flux tubes. With increasing flux, the strong fields form a network on a mesoscale, with thin sheets in the downflow lanes (see Fig. 2) and micropores at the vertices where several lanes merge. As B0 grows, the granular pattern gets more and more disturbed and the typical horizontal scales of granulation decrease.


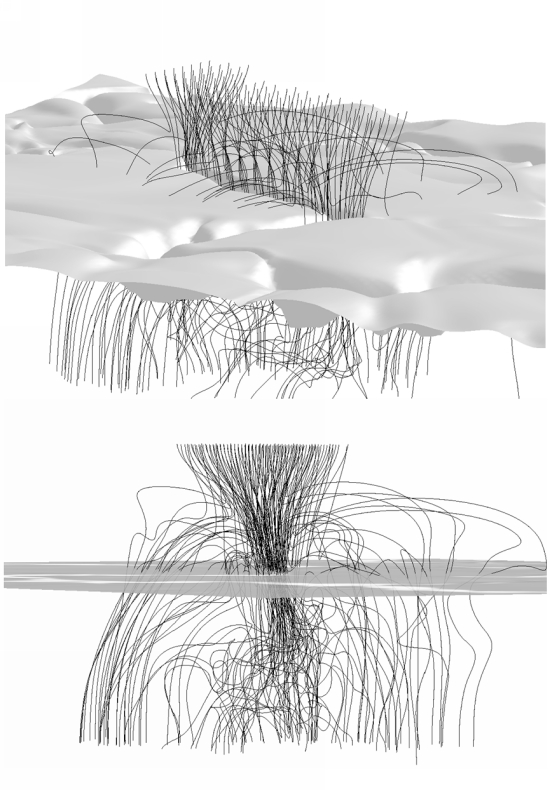
    Figure 2: 3D views of a thin magnetic sheet from two different angles. The shaded surface in the upper panel is the isosurface τRoss = 1. The lower panel shows a face-on view. The sheet loses its coherence in the subsurface layers as the field lines get distorted by vigorous convective flows.

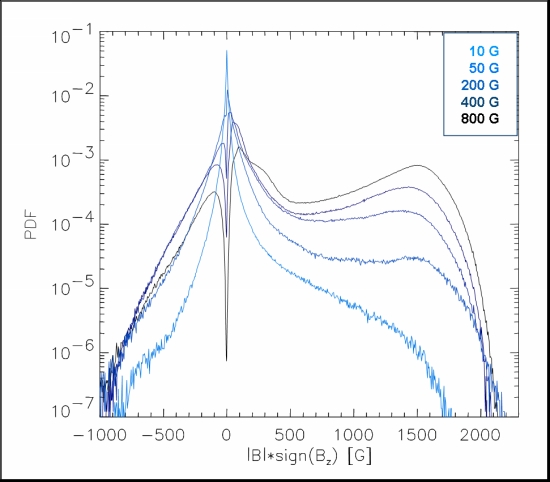
    Figure 3: Probability density functions (PDF) of the magnetic field strength around <τ> = 1. The distribution of the weak fields is a (stretched) exponential. The strong field wing grows with increasing B0 and is Gaussian. In the 10 G run, the maximum field strength around <τ> = 1 is significantly reduced. This finding is independent of grid resolution and shows that the efficiency of convective field amplification is reduced for small, optically thin flux concentrations.

    Reference

    -> back to top

    Decay of bipolar fields in the solar surface layers

    (A. Vögler, R. Cameron, M. Schüssler)

    In a complementary line of simulations we studied the structure and evolution of bipolar magnetic fields in the photosphere and uppermost layers of the convection zone.


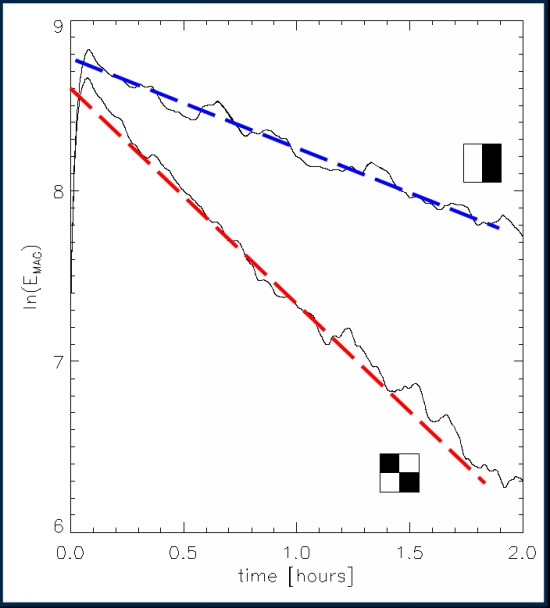
    Figure 1: Exponential decay of the magnetic energy for two mixed-polarity runs with different initial configurations of the bipolar magnetic field ("checkerboard" and "striped"). The decay rates are consistent with the assumption of an effective "turbulent" diffusivity ηt = 1.5 x 1012 cm2/s acting on the fundamental Fourier modes of the respective field configurations.


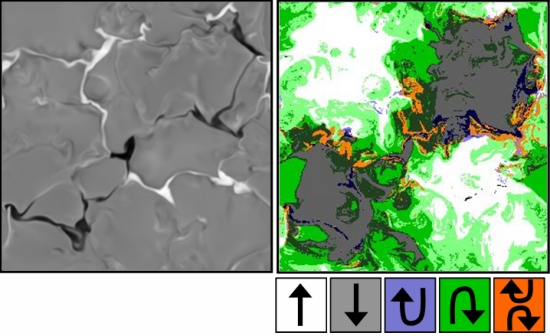
    Figure 2: Left panel - Greyscale magnetogram of the "checkerboard" run at <τ> = 1, 20 minutes after the start of the simulation. The initial configuration is still clearly visible. Right panel - Classification of the magnetic field in four different topology classes: "up", "down", "U-loop", and "inverse U-loop". Flux cancellation requires transformation of the initial "up" and "down" flux into "U-loop" and "inverse U-loop" flux by reconnection. We find that most of the reconnection occurs in the upper photosphere where strong flux concentrations of opposite polarity occasionally get into contact as they move in the intergranular downflow-network in a random-walk style. Accordingly, most of the "reconnected" flux around <τ> = 1 and below occurs in form of inverse U-loops (green in Fig. 2, right panel). Significant amounts of U-loop flux (blue) are only found in the upper photosphere

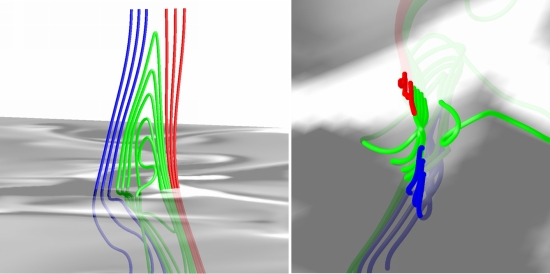
    Figure 3: Field line plot of a reconnection event in the upper photosphere. Left panel: side view; Right panel: top view. The translucent plane shows the vertical field strength at <τ> = 1.

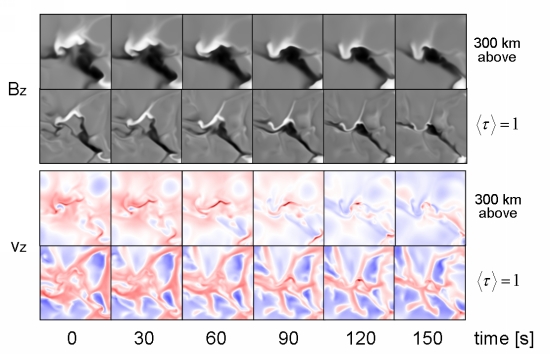
    Fig.4: Time series of a flux-cancellation event. Upper two rows: Vertical magnetic field at <τ> = 1 and 300 km above (strong fields of either polarity are white and black, respectively). Lower two rows: Vertical velocity (blue: upflow, red: downflow). Each panel has a horiztonal extent of 2 x 2 Mm. Owing to the expansion with height, strong field concentrations of opposite polarity first touch in the upper photosphere when moved into each other by convective flows. The time series shows a clear downflow signature 300 km above <τ> = 1 at the current sheet separating the two polarities. The downflow is triggered by the magnetic tension force of inverse U-loops retracting into the underneath layers. A weaker downflow signature is observed at <τ> = 1 with a time lag of about one minute.

    -> back to top

    Simulation of solar pores

    (R. Cameron, A. Vögler, M. Schüssler)


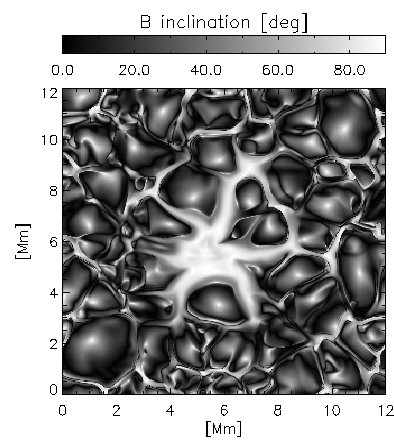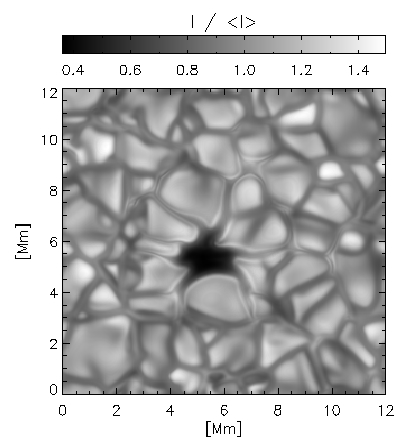
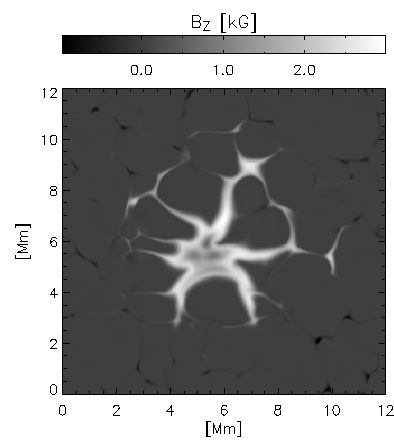
    Figure 1: Pore properties at <τ> = 1. The top left panel shows a continuum brightness image, the panel above shows the vertical field strength and the left panel shows the magnetic field inclination.


    We have used the MURaM code to simulate a solar pore, in order to look at its structure and evolution. Since the model incorporates realistic physics for the photospheric layers, our simulations reproduce both qualitatively (Figure 1) and quantitatively (Figure 2) the properties of pores. This ability to reproduce the observations extends to observations away from disk centre (Figure 3).
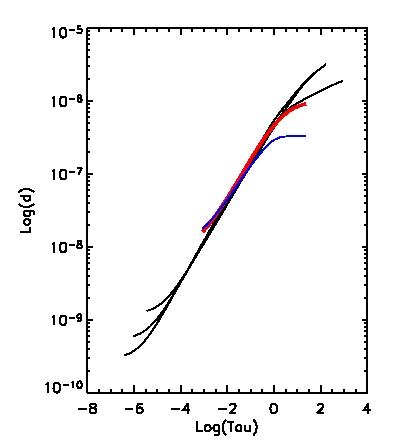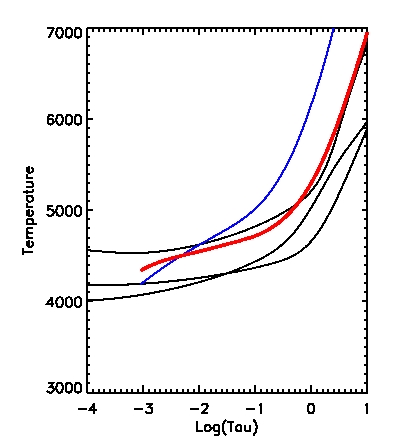    Figure 2a: Height dependence of density as a function of optical depth in the pore. The three black curves are from Sütterlin (observations), the red curve is from a snapshot of our simulated pore, and the blue curve is our simulated quiet sun. Figure 2b: Height dependence of temperature as a function of optical depth in the pore. The three black curves are from Sütterlin (observations), the red curve is from a snapshot of our simulated pore, and the blue curve is our simulated quiet sun.


    Figure 3: A side glance at the pore.
    Having reproduced the observations, we are then in a position to do what is observationally impossible - look beneath the surface of the Sun and directly at the magnetic field lines (Figure 4). In this way we can understand how the physics which determine the form of the pore.
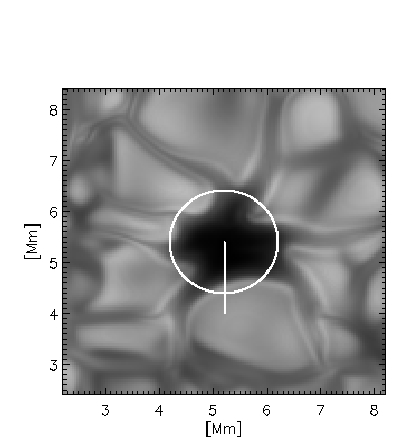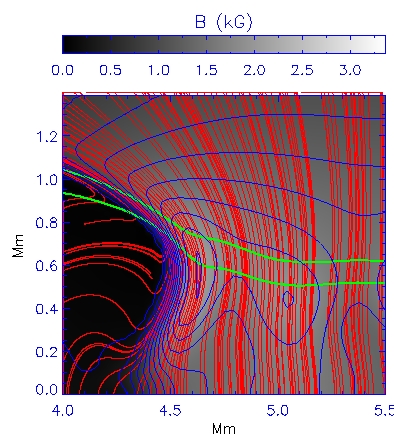
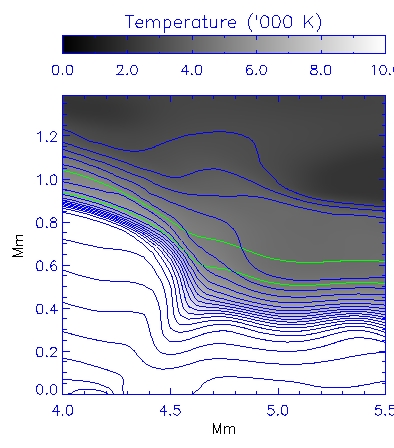
    Figure 4: Shown in the upper left are the magnetic field strength (grey scale and blue contours), the <τ>=1 and 0.1 surfaces (green lines), and the direction of the magnetic field in the plane (blue streaks). The upper right panel shows the temperature structure, whilst the left panel shows the position of this slice.

    Reference

  • Radiative magnetohydrodynamic simulations of solar pores, Cameron, R., Schüssler, M., Vögler, A., Zakharov, V., Astron. Astrophys., in press
  • The decay of a simulated pore, R. Cameron, A. Vögler, S. Shelyag, M. Schüssler, in ASP Conference Series, Vol. 325, 2004.

    -> back to top

    		•

    Magnetic flux emergence

    (M. Cheung, M. Schüssler)


    Figure 1: The footprint of emerging flux - Shown here is a brightness image of the photosphere from a simulation of an emerging flux tube. The emergence event is marked by the transient appearance of an elongated dark lane.


    Magnetic flux emergence on the solar surface takes place over a wide range of fluxes and spatial scales. Studies of the emergence properties of bipolar active regions (Φ ∼ 1022 - 1023 Mx) and ephemeral regions (Φ = (3 - 300)×1018 Mx) indicate that magnetic flux at the larger length scales (10 - 102 Mm) emerge as coherent bundles of magnetic flux, commonly referred to as magnetic flux tubes.

    We study the emergence process by means of numerical MHD simulations. For a proper treatment of the problem, it is important that the simulation code captures the essential physical ingredients in the photosphere, namely radiative transfer, partial ionization, and compressibility. The MURaM code satisfies all these requirements, and allows us to directly compare our simulation results with real photospheric observations of flux emergence. For example, Figure 1 shows a brightness image of a region of the photosphere (simulated) where a flux tube has just emerged. The site of emergence is marked by an elongated dark lane.
  • Magnetic flux emergence in granular convection: radiative MHD simulations and observational signatures, Cheung, M. C. M.; Schüssler, M.; Moreno-Insertis, F., Astron. Astrophys., 467, 703-719 (2007).

    -> back to top

    		•

    Non-grey radiative transfer in radiative MHD simulations

    (A. Vögler, M. Schüssler)

    Radiative transfer in realistic photospheric MHD simulations needs to take into account the effect of line opacities in the middle and upper photosphere. Owing to the sheer number of lines, the modelling of these non-grey effects is statistical in nature.

    Non-grey radiative transfer in the MURaM code makes use of the opacity binning concept which divides the opacity spectrum into a handful (typically 4-5) of classes (bins) according to the opacity strength ("strong lines", "weak lines", "continuum", etc.) Based on a 1D reference atmosphere, the frequencies are classified according to the geometrical height where<τ>ν = 1 is reached (Fig. 1). This way each bin contains frequencies whose main contribution to the radiative heating rate lies in the same height range.

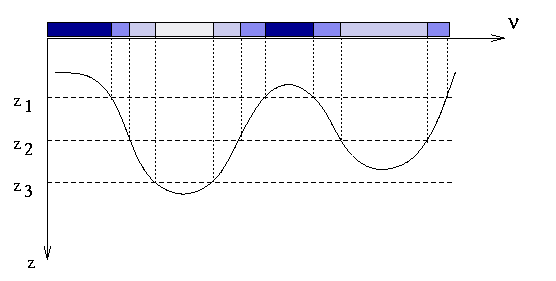    Figure 1: The assignment of frequencies to bins is based on the (frequency-dependent) optical depth scale τν. Frequencies, for which τν = 1 is reached in the same range of geometrical depth z, are assigned to the same bin. The solid line marks the geometrical depth at τν = 1 as a function of frequency.


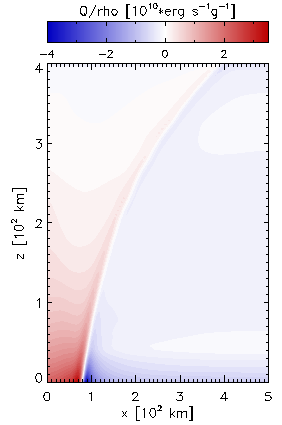
    Test calculations in a static 2D flux-sheet model show that opacity binning does a rather good job of approximating the reference solution obtained with high frequency resolution. It turns out that the advantage over the grey appoach is particularly pronounced in situations where inhomogeneities of the atmosphere lead to lateral heating and cooling effects (Fig. 2). Owing to the inadequate representation of line opacities, the grey radiative transfer is unable to capture these effects and results in qualitatively wrong radiative heating rates. Thus, non-grey radiative transfer modelling is particularly important in MHD simulations which include strong magnetic flux concentrations, because the partial evacuation of these fields leads exactly to the kind of lateral inhomogeneities where the grey approach fails.
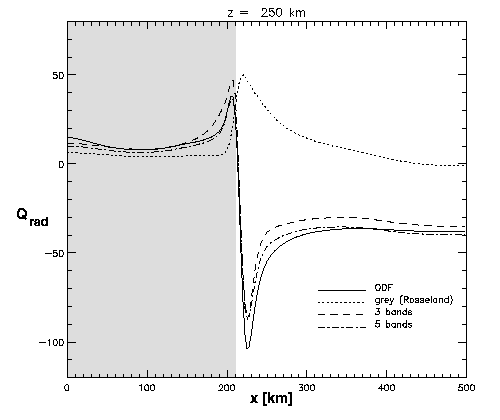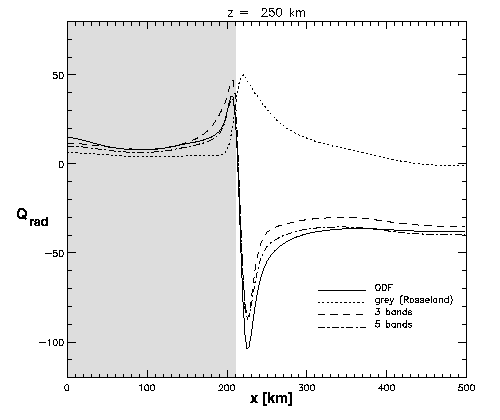
    Figure 2a: Reference solution of Qrad in a magnetic flux-sheet model, obtained with high frequency resolution. Figure 2b: Horizontal cut at a height of z=300 km. The shaded region marks the interior of the flux-sheet. While the opacity binning models perform rather well, grey radiative transfer leads to qualitatively wrong heating rates.

    Consequently, MURaM magneto-convection simulations carried out with a four-bin non-grey radiative transfer significantly differ from grey simulations in the height range τ ≤ 1:

    • The average non-grey temperature profile differs from the grey profile in the optically thin part of the computational domain. It shows the backwarming and line cooling effects that are a familiar property of static 1D radiative equilibrium atmospheres.

    • The non-grey radiative transfer enhances the effect of radiative illumination in magnetic flux concentrations (See Fig. 3).

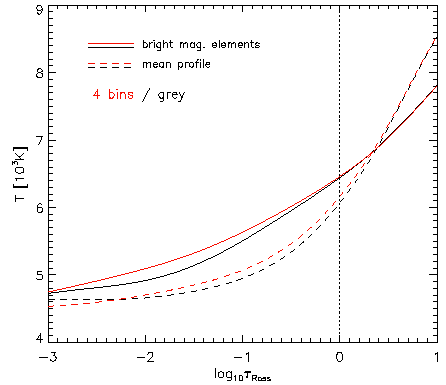
      Figure 3: Solid lines show the vertical temperature profiles inside magnetic structures with above-average brightness. Dashed lines show the mean temperature profiles of the whole simulated domain. Red lines correspond to the non-grey, black ones to the grey simulation run.


    • The use of a non-grey radiative transfer leads to a significant decrease of temperature fluctuations in the upper photosphere (Fig. 4). In the grey case, the Rosseland mean underestimates the strength of absorbers and does not allow an adequate modelling of the smoothing effects of the radiative transfer. The difference is particularly pronounced in magnetic field concentrations.

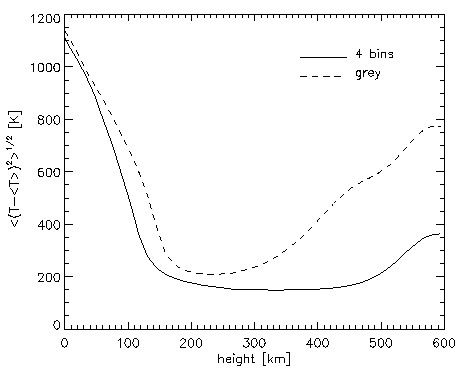
      Figure 4: Vertical profiles of the horizontally averaged temperature fluctuations inside strong magnetic flux concentrations. The non-grey radiative energy exchange strongly reduces temperature fluctuations in the upper photosphere.


    • The differences in the temperature structure affect the appearance of the simulations in brightness maps: the rms intensity contrast is reduced to 15% in the non-grey case compared with 18% in the grey case. This reduction of the overall contrast leads to a contrast enhancement of bright magnetic elements (Fig. 5).

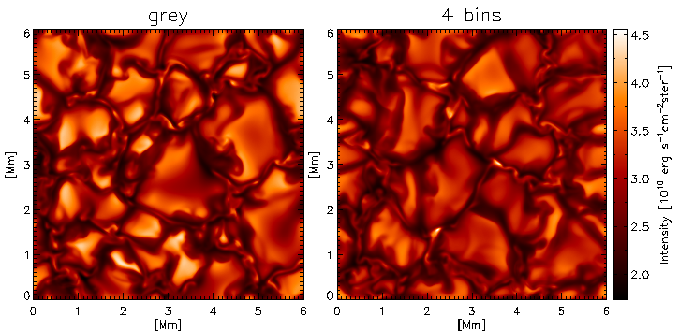
      Figure 5: Maps of frequency-integrated intensity for the grey ( left panel) and non-grey ( right panel) simulation runs, using the same color coding for both images. In the non-grey case, granules are darker and the overall contrast is reduced. As a result, bright magnetic features stand out more prominently.


    Reference

    -> back to top

    Contact: Robert Cameron